Finding Points in a Period-2 Solution of a Difference Equation

• Research
• Open Access
• Published: 09 January 2020

Boundedness of solutions and stability of certain second-order difference equation with quadratic term

Advances in Difference Equations volume 2020, Article number:19 (2020) Cite this article

Abstract

We consider the second-order rational difference equation

$$ {x_{n+1}=\gamma +\delta \frac{x_{n}}{x^{2}_{n-1}}}, $$

where γ, δ are positive real numbers and the initial conditions \(x_{-1}\) and \(x_{0}\) are positive real numbers. Boundedness along with global attractivity and Neimark–Sacker bifurcation results are established. Furthermore, we give an asymptotic approximation of the invariant curve near the equilibrium point.

Introduction and preliminaries

In this paper we consider the following second-order rational difference equation, where we introduce the quadratic term into the denominator

$$ x_{n+1}=\gamma +\delta \frac{x_{n}}{x^{2}_{n-1}},\quad n=0,1, \dots. $$

(1)

We assume that \(\gamma ,\delta >0\) and initial conditions \(x_{-1}\), \(x _{0}\) are positive real numbers. It is convenient to introduce the change of variable

$$ {y_{n}=\frac{x_{n}}{\gamma }}. $$

(2)

This change of variable transforms Eq. (1) into the equation

$$ x_{n+1}=1+p\frac{x_{n}}{x^{2}_{n-1}},\quad n=0,1,\dots , $$

(3)

where \(p=\delta /\gamma ^{2}>0\).

The linear rational version of Eq. (3),

$$ x_{n+1}=a+\frac{x_{n}}{x_{n-1}}, \quad n=0,1,\ldots , $$

(4)

was considered in [1], where the authors proved that the unique positive equilibrium \(\bar{x}=a+1\) is globally asymptotically stable. In [2], the authors investigated Eq. (4) but with quadratic terms in both the numerator and denominator. More precisely, they considered the following equation:

$$ x_{n+1}=a+\frac{x_{n}^{2}}{x_{n-1}^{2}},\quad n=0,1,\ldots. $$

(5)

They proved that the unique positive equilibrium \(\bar{x}=a+1\) is globally asymptotically stable if \(a>\sqrt{2}\). Also, they computed the direction of the Neimark–Sacker bifurcation. We can see that the introduction of quadratic terms into Eq. (4) changes the character of local stability and, consequently, the global dynamics as well.

An elementary calculation shows that Eq. (3) has the unique positive equilibrium point

$$ \bar{x}= (\sqrt{4 p+1}+1 )/2. $$

(6)

In this paper we prove that the parameter space splits into three regions given by \(p<2\), \(p>2\), and \(p=2\). By using a result from [3], we obtain a global result in the case \(p\leq \frac{1+ \sqrt{2}}{2}\). We conjecture that the equilibrium point (6) is globally asymptotically stable for \({p<2}\). To obtain a sequence of invariant and attractive sets that contain all solutions in the case \(1< p<\infty \), we use the technique that is similar to those used in [4, 5] and [6]. This technique is a special case of the so-called Kobayashi metric mentioned in [6]. Namely, we construct a one-parameter family \(\mathcal{S}_{t}\) of compact sets invariant for all t such that \(t_{0}(p)\leq t<\infty \), for some \(t_{0}(p)>\bar{x}\). Figure 1 shows a typical set \(\mathcal{S}_{t}\). The boundary consists of four linear segments \(\overline{P_{1}P_{2}}\), \(\overline{P _{2}P_{3}}\), \(\overline{P_{3}P_{4}}\), \(\overline{P_{4}P_{5}}\) and the curve \(\mathcal{C}_{51}\), which is the part of a parabola joining the points \(P_{1}\) and \(P_{5}\). By using such a construction, it can be shown that any image of a bounded subset of \(\mathbb{R}^{2}\) under the map T is contained in a T-invariant compact set, see [1, 7, 8]. In the case \(p=2\), Neimark–Sacker bifurcation occurs, and we approximate the invariant curve near the positive equilibrium point. For the case \(p>2\), it is easy to see that the equilibrium point (6) is a repeller.

Figure 1

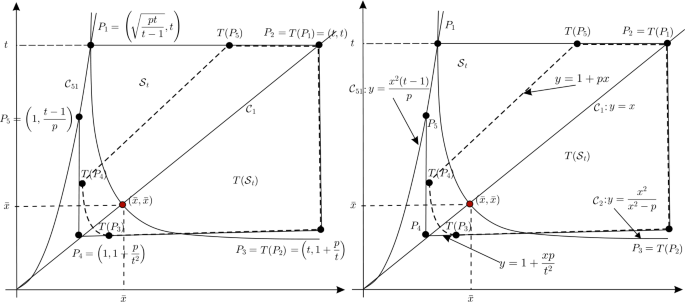
The boundary of a set \(\mathcal{S}_{t}\) (solid) and its image \(T(\partial \mathcal{S}_{t})\) (dashed)

Full size image

The paper is structured as follows. In Sect. 2, a local analysis of the positive equilibrium is performed. In Sect. 3 we present some results about semicycle character of solutions of Eq. (3). Section 4 contains the global stability analysis of the positive equilibrium in the case \(p\leq \frac{1+\sqrt{2}}{2}\). A proof of boundedness of solutions of Eq. (3) for \(1< p<\infty \) is presented in Sect. 5. Section 6 gives a reduction to the Birkhoff normal form and computation of the coefficients of the Neimark–Sacker bifurcation and the asymptotic approximation of the invariant curve near the positive equilibrium point of Eq. (3).

Linearized stability

In this section, we perform a local stability analysis of the positive equilibrium of Eq. (3).

Set

$$ f(u,v)=1+p\frac{u}{v^{2}} $$

and observe that

$$ f_{u}(u,v)=\frac{p}{v^{2}} $$

and

$$ f_{v}(u,v)=-\frac{2pu}{v^{3}}. $$

If x̄ denotes an equilibrium point of Eq. (3), then the linearized equation associated with Eq. (3) about the equilibrium point x̄ is

$$ z_{n+1}=pz_{n}+qz_{n-1}, $$

where

$$ p=f_{u}(\bar{x},\bar{x}) \quad \text{and}\quad q=f_{v}(\bar{x},\bar{x}). $$

(7)

Now, the linearized equation of Eq. (3) at the equilibrium point \({\bar{x}=\frac{1}{2} (\sqrt{4 p+1}+1 )}\) has the following form:

$$ z_{n+1}=\frac{p}{\bar{x}^{2}}z_{n}- \frac{2p}{\bar{x}^{2}}z_{n-1},\quad n=0,1,\dots. $$

(8)

The characteristic equation associated with Eq. (8) is given by

$$ \lambda ^{2}-\frac{p}{\bar{x}^{2}}\lambda + \frac{2p}{\bar{x}^{2}}=0. $$

(9)

By using Theorem 1.1.1 in [1] it is easy to see that the following linearized stability result holds:

Theorem 1

Assume \(p>0\). Then the equilibrium point \({\bar{x}=\frac{1}{2} (\sqrt{4 p+1}+1 )}\) of (3) is

1. (i)

   Locally asymptotically stable if \({p<2}\).

2. (ii)

   A repeller if and only if \({p>2}\).

3. (iii)

   A non-hyperbolic equilibrium if and only if \({p=2}\).

Semicycle analysis

In this section, we present some results about the semicycle character of solutions of Eq. (3). See [1, 9] for more about semicycle analysis.

Consider the following second order difference equation:

$$ x_{n+1}=x_{n}h(x_{n}, x_{n-1}),\quad n=0,1,\ldots. $$

(10)

The following result holds.

Theorem 2

Assume

1. (i)

   \(h\in [(0,\infty )\times (0,\infty ),(0,\infty )]\);

2. (ii)

   \(xh(x,y)\) is increasing in x and decreasing in y;

3. (iii)

   \(h(x,y)\) is decreasing in each argument;

4. (iv)

   \(xh(x,x)\) is decreasing in x;

5. (v)

   The equation

   $$ x_{n+1}=x_{n} h(x_{n},x_{n-1}),\quad n=0,1,\dots , $$

   has a unique positive equilibrium x̄.

Then the following holds:

1. (i)

   If \(x_{N-1}<\bar{x}\leq x_{N}\) (respectively, \(x_{N}\leq \bar{x}< x_{N-1}\)), then \(\bar{x}\leq x_{N+1}\) (respectively, \(x_{N+1}\leq \bar{x}\)).

2. (ii)

   If \(\bar{x}\leq x_{N-1},x_{N}\) (respectively, \(x_{N}, x _{N-1}\leq \bar{x}\)), then \(x_{N+1}\leq x_{N}\) (respectively, \(x_{N+1}\geq x_{N}\)). Moreover, except in the case \(x_{N-1}=x_{N}= \bar{x,}\) the inequalities are strict. Furthermore, if \(x_{N}\leq x _{N-1}\) (respectively, \(x_{N-1}\leq x_{N}\)) then \(x_{N+1}<\bar{x}\) (respectively, \(\bar{x}< x_{N+1}\)).

3. (iii)

   If \(\bar{x}\leq x_{N-1}, x_{N}, x_{N+1}\) (respectively, \(x_{N}, x_{N-1},x_{N+1}\leq \bar{x}\)), then \(x_{N+2}\leq \bar{x}\) (respectively, \(\bar{x}\leq x_{N+2}\)).

4. (iv)

   Except possibly for the first semicycle, every semicycle contains two or three terms.

5. (v)

   The extreme in each semicycle occurs at either the first or the second term.

Proof

We only give the proof for positive semicycles whose terms are not equal to the equilibrium x̄. The proof for negative semicycles is similar and will be omitted. The proof for the trivial semicycle is obvious.

1. (i)

   Assume that \(N\geq 0 \) is such that \(x_{N-1}<\bar{x}\leq x _{N}\). Then, by using assumption (iv), we have

   $$ x_{N+1}=x_{N} h(x_{N},x_{N-1})> \bar{x}f(\bar{x},\bar{x})=\bar{x}, $$

   so \(x_{N+1}\) is also in the same semicyle.

2. (ii)

   Assume that \(N\geq 0 \) such that \(\bar{x}\leq x_{N-1}, x _{N}\). Then (iii) implies

   $$ x_{N+1}=x_{N} h(x_{N},x_{N-1})< x_{N} h(\bar{x},\bar{x})=x_{N}. $$

   Assume that \(x_{N}\leq x_{N-1}\) then (iii) and (iv) imply

   $$ x_{N+1}=x_{N} h(x_{N},x_{N-1}) \leq x_{N} h(x_{N},x_{N})< \bar{x} h( \bar{x},\bar{x})=\bar{x}. $$

3. (iii)

   Assume that \(N\geq 0 \) such that \(\bar{x}\leq x_{N-1}, x _{N}, x_{N+1}\). Then by statement (ii), we have \(x_{N+1}\leq x_{N}\). Now, assumptions (ii) and (iv) imply

   $$ x_{N+2}=x_{N+1} h(x_{N+1},x_{N}) \leq x_{N+1} h(x_{N+1},x_{N+1})< \bar{x} h( \bar{x},\bar{x})=\bar{x}. $$

The rest of the proof follows from (i)–(iii). □

It is obvious that Eq. (3) can be rewritten in the following form:

$$ x_{n+1}=x_{n} \biggl( \frac{1}{x_{n}}+\frac{p}{x_{n-1}^{2}} \biggr) . $$

(11)

Set

$$ h(x_{n}, x_{n-1})=\frac{1}{x_{n}}+ \frac{p}{x_{n-1}^{2}}. $$

It is easy to see that this function h satisfies all the conditions of Theorem 2, which implies that all statements hold. Now, we have the following corollary of Theorem 2.

Corollary 1

Assume that \(p>0\). Then for Eq. (3) the following holds true:

1. (i)

   Except possibly for the first semicycle, every semicycle contains two or three terms.

2. (ii)

   The extreme in each semicycle occurs at either the first or the second term.

3. (iii)

   Every nontrivial solution is strictly oscillatory about the equilibrium x̄.

4. (iv)

   Equation (3) does not have any period 2 or period 3 point in \((0,+\infty )\).

Global asymptotic stability analysis

The following lemma details an invariant interval of Eq. (3).

Lemma 1

Equation (3) possesses an invariant interval only if \(0< p<1\). The interval \([1,\frac{1}{1-p} ]\) is an invariant and attractive set.

Proof

Assume that interval \([L,U]\), \(0< L< U\) is an invariant interval. Then by using the monotonicity of function f, for \(u,v\in [L,U]\), we have

$$ L< f(L,U)\leq f(u,v)< f(U,L)\leq U $$

which is equivalent to

$$ U \bigl(p-L^{2} \bigr)+L^{2}\leq 0 \quad \text{and}\quad (L-1) U^{2}-L p \leq 0. $$

It is easy to see that

$$ \frac{1}{2} L \bigl(L+1-\sqrt{(L-1) (L+3)} \bigr)< 1 $$

for \(1< L<\frac{3}{2}\), hence \(0< p<1\). Straightforward calculations show that \([1,\frac{1}{1-p} ]\) is an invariant and attractive set. □

Notice that Lemma 1 implies that Eq. (3) does not posses an invariant and attractive set for \(p>1\). Also, it is easy to see that in the interval \([1, \frac{1}{1-p} ]\) we can apply Theorem 1.4.5 (see Sect. 1.4. of the monograph [1] or paper [10]) and obtain an attractivity result. Since an invariant interval does not exist for \(p>1\), it is not possible to obtain an attractivity result by applying Theorem 1.4.5.

Because of the above discussion, we apply Lemma 3.3 and Theorem 2.1 in [3] to obtain a global attractivity result of Eq. (3) for \(p\leq \frac{1+\sqrt{2}}{2}\). For this purpose, we substitute the following equation:

$$ x_{n}=1+p\frac{x_{n-1}}{x^{2}_{n-2}} $$

into Eq. (3) and get

$$ x_{n+1}=1+\frac{p}{x_{n-1}^{2}}+ \frac{p^{2}}{x_{n-2}^{2} x_{n-1}}. $$

(12)

Observe now that every solution of Eq. (3) is also a solution of Eq. (12), with initial values \(x_{-2}\), \(x_{-1}\) and \(x_{0}=1+p\frac{x_{0}}{x^{2}_{-1}}\).

Remark 1

Notice that every solution of Eq. (12) satisfies the following inequality:

$$ 1\leq x_{n}\leq 1+p+p^{2},\quad n=1,2,\ldots , \text{for } p>0, $$

which implies that every solution of Eq. (3) is bounded.

Observe also that Eq. (12) is of the form \(x_{n+1}=g(x_{n-2},x _{n-1})\) where

$$ g(x,y)=1+\frac{p}{y^{2}}+\frac{p^{2}}{x^{2} y}. $$

Set

$$ G(x)=g(x,x)=1+\frac{p}{x^{2}}+\frac{p^{2}}{x^{3}}= \frac{p^{2}+p x+x ^{3}}{x^{3}}. $$

(13)

Notice that equations (3) and (12) have the same unique positive equilibrium \(\bar{x}= \frac{1}{2} (\sqrt{4 p+1}+1 )\). Hence, to prove the global attractivity of equilibrium point x̄ of Eq. (3), it is sufficient to prove the global attractivity of x̄ of Eq. (12). The following theorem holds.

Theorem 3

Assume that \({p\leq \frac{1+\sqrt{2}}{2}}\). Then the unique positive equilibrium of (3) is globally asymptotically stable.

Proof

First, computing the first-order partial derivatives of g, it is easy to see that

$$ \frac{\partial g}{\partial x}(x,y)< 0\quad \text{and}\quad \frac{ \partial g}{\partial y}(x,y)< 0, \quad \text{for all }x,y>0. $$

From

$$ {G'(\bar{x})=-\frac{16 p (3 p+\sqrt{4 p+1}+1 )}{ (\sqrt{4 p+1}+1 )^{4}}} $$

we have \(G'(\bar{x})\geq -1\) if \({p\leq \frac{1+\sqrt{2}}{2}}\). The Schwarzian derivative,

$$ SG(x)=\frac{G'''(x)}{G'(x)}-\frac{3}{2} \biggl(\frac{G''(x)}{G'(x)} \biggr) ^{2}, $$

is given by

$$ SG(x)=- \frac{6 (6 p^{2}+4 p x+x^{2} )}{x^{2} (3 p+2 x)^{2}}, $$

and it is obvious that

$$ SG(x)< 0, \quad \text{for all } x\geq 0. $$

Therefore, by Lemma 3.3 and Theorem 2.1 in [3], equilibrium x̄ is a global attractor of all positive solutions of Eq. (12), and hence is also a global attractor of all positive solutions of Eq. (3). □

Attractive set for solutions

In this section, we give a construction of a sequence of invariant and attractive sets that contain all solutions. The main result of this section is Theorem 5 concerning attractive sets for solutions of Eq. (3).

Throughout the section we shall assume the inequality

The change of variables \(u_{n}=x_{n-1}\) and \(v_{n}=x_{n}\) transforms Eq. (3) into the system of difference equations:

$$ \textstyle\begin{cases} u_{n+1} = v_{n}, \\ v_{n+1} = 1+p\frac{v_{n}}{u_{n}^{2}}. \end{cases} $$

(14)

The map T corresponding to system (14) is given by

It is obvious that \(T(\mathbb{R}_{+}^{2})\subset (1,\infty )\times (1, \infty )\) and \(T((1,\infty )\times (1,\infty ))\subset (1,\infty ) \times (1,\infty )\), so it is sufficient to consider the map T on the set \(\mathcal{K}=(1,\infty )\times (1,\infty )\). Let \(T=(T_{1},T_{2})\). The equilibrium curves of T are the following sets:

$$ \mathcal{C}_{1}:=\big\{ (x,y)\in \mathcal{K}:T_{1}(x,y)=x\big\} \quad \text{and}\quad \mathcal{C}_{2}:=\bigl\{ (x,y)\in \mathcal{K}:T _{2}(x,y)=y\bigr\} . $$

It is easy to see that the equilibrium curves are as follows:

$$ \mathcal{C}_{1}:=\bigl\{ (x,y)\in \mathcal{K}:y=x\bigr\} \quad \text{and}\quad \mathcal{C}_{2}:= \biggl\{ (x,y)\in \mathcal{K}:x= \sqrt{\frac{p y}{y-1}} \biggr\} . $$

Assume that t is any parameter such that \(t>\bar{x}\). Since \(\bar{x}>1\), we have \(t>1\). This implies that assumption \(t>\bar{x}\) is equivalent to \(t^{2}-t-p>0\).

Now, consider the following five points, see Fig. 1:

$$ \begin{aligned}&P_{1}= \biggl(\sqrt{\frac{p t}{t-1}},t \biggr),\qquad P_{2}=(t,t),\qquad P_{3}= \biggl(t,1+\frac{p}{t} \biggr), \\ & P_{4}= \biggl(1,1+\frac{p}{t^{2}} \biggr),\qquad P_{5}= \biggl(1,\frac{t-1}{p} \biggr). \end{aligned}$$

Denote with \(\preceq _{ne}\) the northeast partial ordering on \(\mathbb{R}^{2}\) whose nonnegative cone is the standard first quadrant \(\{(u,v): u, v\geq 0\}\). That is, \((u_{1}, v_{1})\preceq _{ne} (u _{2}, v_{2})\) if and only if \(u_{1}\leq u_{2}\) and \(v_{1} \leq v_{2}\), see [11]. The following lemma holds.

Lemma 2

The following statements hold true.

1. (i)

   \(P_{1}\preceq _{ne}P_{2}\), \(P_{3}\preceq _{ne}P_{2}\), \(P_{4}\preceq _{ne}P_{3}\), \(P_{4}\preceq _{ne}P_{5}\).

2. (ii)

   Assume that \(t^{3}-(p+1)t^{2}-p^{2}>0\), then \(P_{5}\preceq _{ne}P_{1}\).

Proof

Notice that \(P_{1}\preceq _{ne} P_{2}\) is equivalent with \(t^{2}-t-p>0\) which is true since \(t>\bar{x}\). Since \(t>1\) and \(p>1 \) it is obvious that \(P_{3}\preceq _{ne}P_{2}\), \(P_{4}\preceq _{ne} P_{3}\) and \(P_{5}\preceq _{ne} P_{1}\). Only, we have to check that \(P_{4}\preceq P_{5}\). This is equivalent to

$$ 1+\frac{p}{t^{2}}\leq \frac{t-1}{p}, $$

which is true if and only if \(t^{3}-t^{2} (1+p)-p^{2}\geq 0\). □

Denote by \(\overline{P_{i}P_{j}}\) the line segment joining points \(P_{i}\) and \(P_{j}\) for \(1\leq i,j\leq 5\), \(i\neq j\).

Let

$$ \mathcal{C}_{51}:= \biggl\{ \biggl(x,\frac{x^{2}(t-1)}{p} \biggr):1 \leq x\leq \sqrt{\frac{p t}{t-1}} \biggr\} $$

be the part of parabola

$$ y=\frac{x^{2}(t-1)}{p} $$

between \(P_{5}\) and \(P_{1}\).

Let \(\mathcal{S}_{t}\) be set consisting of four line segments \(\overline{P_{i}P_{j}}\) and curve \(\mathcal{C}_{51}\), namely of

$$ \overline{P_{1}P_{2}}, \overline{P_{2}P_{3}}, \overline{P_{3}P_{4}},\overline{P _{4}P_{5}}, \mathcal{C}_{51}, $$

as in Fig. 1.

To prove some properties of images of the line segments \(\overline{P _{i}P_{j}}\) and curve \(\mathcal{C}_{51}\), we shall employ the resultant of two polynomials, see [12, 13]. Let \(f_{1}(x)=a_{n}x^{n}+a _{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}\) and \(g_{1}(x)=b_{m}x^{m}+b_{m-1}x ^{m-1}+\cdots +b_{1}x+b_{0}\) be two polynomials of degrees n and m, respectively. Their resultant \(\operatorname{Res}(f_{1},g_{1})\) is the determinant of the \((m+n)\times (m+n)\) Sylvester matrix given by

Syl ( f_1 , g_1 ) = \left(\begin{array}{cccccccc}{a}_n& a_{n-1}& \dots & a_1& a_0& 0& \dots & 0\\ 0& a_n& a_{n-1}& \dots & a_1& a_0& \dots & 0\\ ⋮& & & & & & & \\ 0& \dots & a_n& a_{n-1}& a_{n-2}& \dots & a_1& a_0\\ b_m& b_{m-1}& \dots & b_1& b_0& 0& \dots & 0\\ 0& b_m& b_{n-1}& \dots & b_1& b_0& \dots & 0\\ ⋮& & & & & & & \\ 0& 0& \dots & b_m& b_{m-1}& b_{m-2}& \dots & b_0\end{array}\right)

or

$$ \operatorname{Res}(f_{1},g_{1})=a_{n}^{m}b_{m}^{n} \prod_{i=1}^{n}\prod _{j=1}^{m} ( \alpha _{i}-\beta _{j} ), $$

where \(\alpha _{i}\), \(i=1,2,\ldots ,n\) and \(\beta _{j}\), \(j=1,2,\ldots ,m\) are the zeros of the polynomials \(f_{1}(x)\) and \(g_{1}(x)\), respectively.

The following lemma holds.

Lemma 3

Let \(f_{1}(x)\) and \(f_{2}(x)\) be two polynomials of degrees \(n\geq 1\) and \(m\geq 1\), respectively. Further, suppose that \(f_{1}(x)\) and \(g_{1}(x)\) each have exactly one positive root \(\alpha _{n}\) and \(\beta _{m}\). Assume that \(a_{n},b_{m}>0\). Then \((-1)^{n-1}(\alpha _{n}-\beta _{m})>0\) if and only if \(\operatorname{res}(f_{1},f_{2})>0\). Furthermore, assume that \(\operatorname{res}(f_{1},f_{2})>0\). If n is odd then \(f_{1}(x)>0 \Rightarrow f_{2}(x)>0\) and if n is even then \(f_{2}(x)>0\Rightarrow f_{1}(x)>0\).

Proof

Since \(\alpha _{n}\) is the only one positive root of \(f_{1}(x)\), and \(\beta _{m}\) is the only one positive root of \(g_{1}(x)\), we have

$$\begin{aligned}& f_{1}(x)=a_{n}(x-\alpha _{n})f_{2}(x), \quad \text{where } f_{2}(x)\geq 0\ \forall x>0, \\& g_{1}(x)=b_{m}(x-\beta _{m})g_{2}(x), \quad \text{where } g_{2}(x)\geq 0\ \forall x>0, \end{aligned}$$

where the leading coefficient of \(f_{2}(x)\) and \(g_{2}(x)\) is one. We have

$$\begin{aligned} \operatorname{Res}(f_{1},g_{1}) =&a_{n}^{m}b_{m}^{n} \prod _{i=1}^{n}\prod _{j=1}^{m} ( \alpha _{i}-\beta _{j} ) \\ =&a_{n}^{m} b_{m}^{n} \prod _{i=1}^{n} ( \alpha _{i}- \beta _{m} )g_{2}(\alpha _{i}) \\ =&a_{n}^{m} b_{m}^{n} \prod _{i=1}^{n} ( \alpha _{i}- \beta _{m} ) \prod_{i=1}^{n} g_{2}(\alpha _{i}) \\ =&a_{n}^{m} b_{m}^{n}(-1)^{n-1} ( \alpha _{n}-\beta _{m} )f_{2}(\alpha _{n}) \prod_{i=1}^{n} g_{2}(\alpha _{i}). \end{aligned}$$

This implies

$$ \operatorname{Res}(f_{1},g_{1})>0\quad \Leftrightarrow\quad (-1)^{n-1}(\alpha _{n}-\beta _{m})>0. $$

Assume that \(\operatorname{Res}(f_{1},g_{1})>0\). Then from the previous conclusion, we have \(\alpha _{n}>\beta _{m}\). Since \(a_{n}, b_{m}>0\), we have that \(f_{2}(x)>0\Leftrightarrow x>\beta _{m}\) and \(f_{1}(x)>0 \Leftrightarrow x>\alpha _{n}\), from which the proof follows. □

Also, we shall need the following two lemmas.

Lemma 4

Assume that \(p>1\). The equation

$$ t^{5}- \bigl(p^{2}+p+1 \bigr) t^{4}+2 p t^{3}-p \bigl(p^{2}+2 \bigr) t^{2}+p^{2} t-p^{2}=0 $$

has exactly one positive root and two pairs of conjugate complex roots.

Proof

Let

$$ \tilde{f}(t)=t^{5}- \bigl(p^{2}+p+1 \bigr) t^{4}+2 p t^{3}-p \bigl(p ^{2}+2 \bigr) t^{2}+p^{2} t-p^{2}. $$

By the Descartes' Rule of Signs, \(\tilde{f}(t)=0\) has no negative roots. The following matrix, called the discrimination matrix of \(\tilde{f}(y)\) and \(\tilde{f}'(y)\), see [14], is actually the Sylvester matrix of \(\tilde{f}(y)\) and \(\tilde{f}'(y)\) with some permuted rows, and is given by

Discr ( \tilde{f} ) = \left(\begin{array}{cccccccccc}1& -B& 2p& -Ap& p^2& -p^2& 0& 0& 0& 0\\ 0& 5& -4B& 6p& -2Ap& p^2& 0& 0& 0& 0\\ 0& 1& -B& 2p& -Ap& p^2& -p^2& 0& 0& 0\\ 0& 0& 5& -4B& 6p& -2Ap& p^2& 0& 0& 0\\ 0& 0& 1& -B& 2p& -Ap& p^2& -p^2& 0& 0\\ 0& 0& 0& 5& -4B& 6p& -2Ap& p^2& 0& 0\\ 0& 0& 0& 1& -B& 2p& -Ap& p^2& -p^2& 0\\ 0& 0& 0& 0& 5& -4B& 6p& -2Ap& p^2& 0\\ 0& 0& 0& 0& 1& -B& 2p& -Ap& p^2& -p^2\\ 0& 0& 0& 0& 0& 5& -4B& 6p& -2Ap& p^2\end{array}\right) ,

where \(A=p^{2}+2\) and \(B=p^{2}+p+1\). Let \(D_{k}\) denote the determinant of the submatrix of \(\operatorname{Discr}(\tilde{f})\), formed by the first 2k rows and the first 2k columns, for \(k=1,\dots ,5\). So, by straightforward calculation one can see that

$$\begin{aligned}& D_{1}(p) =5, \\& D_{2}(p) =4 \bigl(p^{4}+2 p^{3}+3 p^{2}-3 p+1 \bigr), \\& D_{3}(p) =-p \bigl(8 p^{8}+24 p^{7}+64 p^{6}+77 p^{5}+76 p^{4}+100 p ^{3}-24 p^{2}+80 p+16 \bigr), \\& D_{4}(p) =-2 p^{4} \bigl(4 p^{11}+12 p^{10}+32 p^{9}+19 p^{8}-20 p ^{7}-62 p^{6}-120 p^{5} \\& \hphantom{D_{4}(p) =}{}+70 p^{4}-246 p^{3}+178 p^{2}-160 p-32 \bigr) \\& D_{5}(p) =p^{8} \bigl(16 p^{12}+44 p^{11}+84 p^{10}-108 p^{9}-404 p ^{8}-348 p^{7}+384 p^{6} \\& \hphantom{D_{5}(p) =}{}+1856 p^{5}-427 p^{4}+960 p^{3} \\& \hphantom{D_{5}(p) =}{}-480 p^{2}+1536 p+256 \bigr) \end{aligned}$$

One can see that \(D_{3}(p)<0\). By using Theorem 1 in [14] for the polynomial \(D_{5}(p)\), one can see that \(D_{5}\) has five pairs of conjugate complex roots and two negative roots for \(p>1\), which implies \(D_{5}(p)>0\). Then the sign list of the sequence \(\{D_{1}(p),D _{2}(p),D_{3}(p),D_{4}(p),D_{5}(p)\}\) is given by

$$ \bigl[1,1,-1,\operatorname{sign}\bigl(D_{4}(p) \bigr),1\bigr], $$

(16)

from which it follows that the number of sign changes of the revised sign list of the list (16) is two. Now, the statement follows in view of Theorem 1 in [14]. □

Lemma 5

Assume that \(1< p<\infty \). Let

$$ \begin{aligned} &P_{p}^{(1)}(t) :=t^{2}-t-p, \\ &P_{p}^{(2)}(t):=t^{3}-(p+1)t^{2}-p^{2}, \\ &P_{p}^{(3)}(t):=2 t^{3}-p^{2} t^{2}-2 t^{2}+2 p t-2 p, \\ &P_{p}^{(4)}(t):=t^{5}- \bigl(p^{2}+p+1 \bigr) t^{4}+2 p t^{3}-p \bigl(p^{2}+2 \bigr) t^{2}+p^{2} t-p^{2}. \end{aligned} $$

Then \(P_{p}^{(i)}, 1,\dots ,4\), have exactly one positive root and the following holds:

1. (i)

   \(P_{p}^{(2)}(t)>0\Rightarrow P_{p}^{(1)}(t)>0\);

2. (ii)

   \(P_{p}^{(4)}(t)>0 \Rightarrow P_{p}^{(3)}(t)>0\);

3. (iii)

   \(P_{p}^{(4)}(t)>0 \Rightarrow P_{p}^{(2)}(t)>0\).

Proof

By Lemma 4, \(P_{p}^{(4)}(t)\) has exactly one positive root. By the Descartes' Rule of Signs, \(P_{p}^{(1)}(t)\) and \(P_{p}^{(2)}(t)\) have exactly one positive root, and \(P_{p}^{(3)}(t)\) has no negative root. The discriminant of \(P_{p}^{(3)}(t)\) is given by

$$ \tilde{g}(p):=\operatorname{Dis}\bigl(P_{p}^{(3)} \bigr)=-4 p \bigl(2 p^{6}-p ^{5}+12 p^{4}-40 p^{3}+40 p^{2}+32 p+16 \bigr). $$

Since

$$ \tilde{g}(u+1)=-4 (u+1) \bigl(2 u^{6}+11 u^{5}+37 u^{4}+38 u^{3}+12 u ^{2}+47 u+61 \bigr) $$

for \(u>0\), we have \(\operatorname{Dis}(P_{p}^{(3)})<0\) for \(p>1\). This implies that \(P_{p}^{(3)}\) has one pair of conjugate complex roots. Hence, \(P_{p}^{(3)}(t)\) has exactly one positive root.

The rest of the proof follows from the facts:

$$\begin{aligned}& \operatorname{res}\bigl(P_{p}^{(2)},P_{p}^{(1)} \bigr)= 4 p^{4}>0 \quad \text{for }p>0; \\& \operatorname{res}\bigl(P_{p}^{(4)},P_{p}^{(2)} \bigr)= p^{6} \bigl(p^{7}-p^{6}+p^{5}-9 p ^{4}+13 p^{3}-6 p^{2}+4 p-2 \bigr)>0 \quad \text{for }p>1; \\& \operatorname{res}\bigl(P_{p}^{(4)},P_{p}^{(3)} \bigr)= p^{7} \bigl(p^{7}+2 p^{6}-8 p^{4}-16 p^{3}+16 p^{2}+16 p+32 \bigr)>0 \quad \text{for }p>1, \end{aligned}$$

which can be verified in a similar way and by using Lemma 3. □

Lemmas 6 and 7 given below detail the images of line segments \(\overline{P_{i}P_{j}}\) and curve \(\mathcal{C}_{51}\) under the map T.

Lemma 6

Assume that \(1< p<\infty <\) and \(P_{p}^{(2)}(t)>0\) Then the following holds:

1. (i)

   \(T(\overline{P_{1}P_{2}})=\overline{P_{2}P_{3}}\);

2. (ii)

   \(T(\overline{P_{2}P_{3}})\subset \overline{P_{2}P_{4}} \setminus \{P_{4}\}\);

3. (iii)

   \(T(\mathcal{C}_{51})\subset \overline{P_{1}P_{2}}\setminus \{P_{1}\}\).

Proof

1. (i)

   Since \(\overline{P_{1}P_{2}}=\{(1-u)P_{1}+u P_{2}:0\leq u \leq 1\}\), we have

   $$ T(\overline{P_{1}P_{2}})= \biggl\{ \biggl(t, \frac{p t}{ ((1-u) \sqrt{\frac{p t}{t-1}}+t u )^{2}}+1 \biggr):0\leq u\leq 1 \biggr\} =\overline{P_{2}P _{3}}. $$

2. (ii)

   From \(\overline{P_{2}P_{3}}=\{(1-u)P_{2}+u P_{3}:0\leq u \leq 1\}\) we have

   $$ \begin{aligned} T(\overline{P_{2}P_{3}}) &= \biggl\{ \biggl(\frac{p u}{t}-t u+t+u,\frac{p ^{2} u+p t (t+u-t u)+t^{3}}{t^{3}} \biggr):0\leq u\leq 1 \biggr\} \\ &=\bigl\{ (x_{1}(u),y_{1}(u):0\leq u\leq 1\bigr\} . \end{aligned} $$

   Solving \(x_{1}(u)=x\) for u, we obtain

   $$ u=-\frac{t (t-x)}{p-t^{2}+t}. $$

   Substituting this into \(y= y_{1}(u)\), we get

   $$ y=\frac{p x}{t^{2}}+1. $$

   So we obtain

   $$ T(\overline{P_{2}P_{3}})= \biggl\{ \biggl(x, \frac{p x}{t^{2}}+1\biggr): 1+ \frac{p}{t}\leq x\leq t \biggr\} . $$

   Since

   $$ \overline{P_{3}P_{4}}= \biggl\{ \biggl(x, \frac{p x}{t^{2}}+1\biggr): 1\leq x \leq t \biggr\} \quad \text{and}\quad t^{2}-t-p>0, $$

   we obtain \(T(\overline{P_{2}P_{3}})\subset \overline{P_{3}P_{4}} \setminus \{P_{4}\}\).

3. (iii)

   Since \(\mathcal{C}_{51}= \{ (u, \frac{u^{2}(t-1)}{p}):1\leq u\leq \sqrt{\frac{p t}{t-1}} \} \), we obtain

   $$\begin{aligned} T(C_{51}) =& \biggl\{ \biggl(\frac{(t-1) u^{2}}{p},t \biggr):1\leq u \leq \sqrt{\frac{p t}{t-1}} \biggr\} \\ =&\biggl\{ (x_{2}(u),y_{2}(u):1 \leq u \leq \sqrt{\frac{p t}{t-1}}\biggr\} . \end{aligned}$$

   Since \(x_{2}(1)= (\frac{t-1}{p},t )\) and \(x_{2} (\sqrt{\frac{p t}{t-1}} )=(t,t)\), we have that \(T(\mathcal{C}_{51})\subset \overline{P_{1}P_{2}}\setminus \{P_{1}\}\).

 □

Lemma 7

Assume that \(1< p<\infty \) and \(P_{p}^{(4)}(t)>0\). Then the following holds:

1. (i)

   \(T(\overline{P_{3}P_{4}}\setminus \{P_{3}\})\subset \operatorname{int}(\mathcal{S}_{t})\);

2. (ii)

   \(T(\overline{P_{4}P_{5}}\setminus \{P_{5}\})\subset \operatorname{int}(\mathcal{S}_{t})\)

Proof

From (ii) and (iii) of Lemma 5, we have \(2 t^{3}-p^{2} t^{2}+2 p t-2 p-2 t^{2}>0\).

1. (i)

   From \(\overline{P_{3}P_{4}}=\{(1-u)P_{3}+u P_{4}:0\leq u \leq 1\}\) we have

   $$ \begin{aligned} T(\overline{P_{3}P_{4}}) &= \biggl\{ \biggl(\frac{p (t+u-t u)+t^{2}}{t ^{2}}, \frac{p (p (t (-u)+t+u)+t^{2} )}{t^{2} (t+u-t u)^{2}}+1 \biggr):0 \leq u \leq 1 \biggr\} \\ &=\bigl\{ \bigl(x_{3}(u),y_{3}(u)\bigr):0\leq u\leq 1 \bigr\} . \end{aligned} $$

   Solving \(x_{3}(u)=x\) for u, we obtain

   $$ u=\frac{t (p-t x+t)}{p (t-1)}. $$

   Substituting this into \(y= y_{3}(u)\), we get

   $$ y_{3}(x)=\frac{p^{3} x}{t^{4} (x-1)^{2}}+1. $$

   So we obtain

   $$ T(\overline{P_{2}P_{3}})= \biggl\{ \biggl(x, \frac{p^{3} x}{t^{4} (x-1)^{2}}+1 \biggr): \frac{p}{t^{2}}+1\leq x \leq \frac{p}{t}+1 \biggr\} . $$

   It is easy to see

   $$ y'_{3}(x)=-\frac{p^{3} (x+1)}{t^{4} (x-1)^{3}}\quad \text{and}\quad y''_{3}(x)=\frac{2 p^{3} (x+2)}{t^{4} (x-1)^{4}}. $$

   Since

   $$ y_{3} \biggl(\frac{p}{t^{2}}+1 \biggr)=p \biggl( \frac{p}{t^{2}}+1 \biggr)+1, $$

   to show \(T(\overline{P_{2}P_{3}})\subset \overline{P_{2}P_{3}}\) it is enough to prove

   $$ y_{3} \biggl(\frac{p}{t^{2}}+1 \biggr)-\frac{ (\frac{p}{t^{2}}+1 ) ^{2}(t-1)}{p}< 0. $$

   Since

   $$\begin{aligned}& y_{3} \biggl(\frac{p}{t^{2}}+1 \biggr)-\frac{ (\frac{p}{t^{2}}+1 ) ^{2}(t-1)}{p} \\& \quad = \frac{p^{3} t^{2}+p^{2} t^{4}-p^{2} t+p^{2}+p t^{4}-2 p t^{3}+2 p t^{2}-t^{5}+t^{4}}{p t^{4}} \\& \quad =-\frac{P_{p}^{(4)}(t)}{p t^{4}}< 0, \end{aligned}$$

   we have \(T(\overline{P_{3}P_{4}})\subset S_{t}\).

2. (ii)

   One can see that \(T(\overline{P_{4}P_{5}})= \{ (x,1+px):\frac{p}{t ^{2}}+1\leq x \leq \frac{t-1}{p} \} \). Since \(\mathcal{C}_{51}\) is the graph of an increasing, concave up function \(y= \frac{x^{2}(t-1)}{p}\), it is enough to show that its slope at \((\frac{p}{t^{2}}+1,p (\frac{p}{t^{2}}+1 )+1 )\) is not smaller than the slope of the line equation \(y=1+p x\), i.e.,

   $$ \frac{2 (t-1) (\frac{p}{t^{2}}+1)}{p}-p=\frac{2 t^{3}-p^{2} t^{2}+2 p t-2 p-2 t^{2}}{p t^{2}}>0, $$

   which is true by relation (iii) of Lemma 6.

 □

In the sequel let \(t_{0}(p)\) be a unique positive root of the equation (see Lemma 4)

$$ t^{5}- \bigl(p^{2}+p+1 \bigr) t^{4}+2 p t^{3}-p \bigl(p^{2}+2 \bigr) t^{2}+p^{2} t-p^{2}=0. $$

Lemma 8 details elementary properties of sets \(S_{t}\). See Fig. 1.

Lemma 8

Assume that \(1< p<\infty \).

1. (i)

   \((\bar{x},\bar{x})\in \mathcal{S}_{t}\) for \(t_{0}(p)\leq t< \infty \).

2. (ii)

   If \(t_{0}(p)< t'<t<\infty \), then \(\mathcal{S}_{t'}\subset \operatorname{int}(\mathcal{S}_{t})\).

3. (iii)

   If \((1,\infty )^{2}=\cup \{\mathcal{S}_{t}:t_{0}(p) \leq t<\infty \}\).

4. (iv)

   For \((x,y)\notin S_{t_{0}(p)}\) there exists \(t'> t_{0}(p)\) such that \((x,y)\in \partial \mathcal{S}_{t'}\).

Proof

Statement (i) follows from the construction of the set \(\mathcal{S} _{t}\) and the point \(P_{1}\) which belongs to the equilibrium curve \(\mathcal{C}_{2}\). Statement (ii) follows directly from the definition of the set \(\mathcal{S}_{t}\) and Lemmas 7, 6, and 2. Notice that the x-coordinate of the point \(P_{1}\) goes to infinity as t approaches one. Then it is obvious that the union of the sets \(\mathcal{S}_{t}\) covers the set \((1,\infty )^{2}\), from which statement (iii) follows. Statement (iv) follows from (iii) and definition of the set \(\mathcal{S} _{t}\). □

A set R is said to be invariant under the map T if \(T(R)\subset R\).

Lemma 9

Assume that \(1< p<\infty \). The set \(\mathcal{S}_{t}\) is invariant if \(t_{0}(p)\leq t<\infty \). Further \(T^{4}(\mathrm{S}_{t})\subset \operatorname{int}(\mathcal{S}_{t})\).

Proof

It is very easy to see that the map T is \(1-1\) on \((1,\infty )^{2}\). From this and from the fact that \(\mathcal{S}_{t}\) contains the unique positive fixed point of T, it follows that to prove \(\mathcal{S} _{t}\) is invariant, it suffices to show \(T(\partial S_{t})\subset S _{t}\), which follows from Lemmas 6 and 7. The rest of the proof follows from Lemmas 2 and 8. See Fig. 1. □

For \(\mathcal{A}\subset \mathbb{R}_{+}^{2}\) let \(\omega (\mathcal{A})\) denote the omega-limit of \(\mathcal{A}\) under the map T, i.e., the set of all accumulation points of all sequences \(\{T^{n}(x)\}\) for \(x\in \mathcal{A}\).

Lemma 4, given below details the property of the omega limit set.

Theorem 4

Assume that \(1< p<\infty \). Then \(\omega ((0,\infty )\times (0,\infty ))\subset S_{t_{0}(p)}\).

Proof

Let \((x,y)\in (0,\infty )\times (0,\infty )\). Since \(T(x,y)\in (1, \infty )\times (1,\infty )\), we have \(T(x,y)\in \mathcal{S}_{t}\) for some \(t>t_{0}(p)\). By Lemma 9, \(T^{n}(x,y)\in \mathcal{S}_{t}\) for \(n>1\) and \(T^{n}(x,y)\) has at least one accumulation point \((x_{1},y_{1})\). Suppose that \((x_{1},y_{1})\notin S_{t_{0}(p)}\), then by (iv) of Lemma 8 there exists \(t'> t_{0}(p)\) such that \((x_{1},y_{1})\in \partial \mathcal{S}_{t'}\). By continuity of T and by Lemma 9, \(T^{n}(x,y)\in \operatorname{int}(S_{t'})\) for all n sufficiently large. This is not possible since \((x_{1},y_{1})\) is an accumulation point of \(T^{n}(x,y)\). Hence, \((x_{1},y_{1})\in S_{t_{0}(p)}\). □

Now, we state Theorem 5 concerning the attractivity sets for solutions of Eq. (3). The proof of Theorem 5 directly follows from Lemma 8 and Theorem 4.

Theorem 5

For all n sufficiently large, \(T^{n}(x,y)\in S_{t_{0}(p)}\).

Based on numerical visualization, we pose the following conjecture. See Fig. 2.

Figure 2

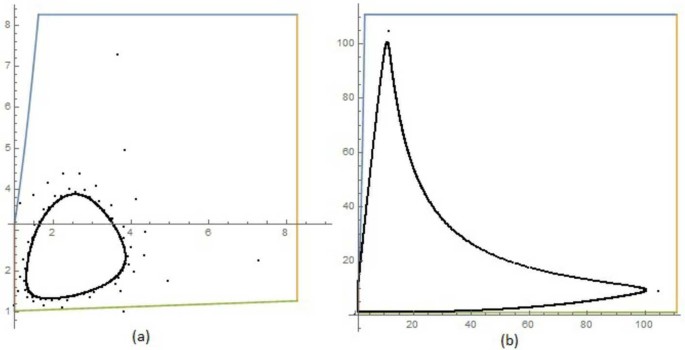
Trajectory of the point \((0.1,0.2)\) and invariant set \(\mathcal{S}_{t}\) for (a) \(p=2.3\) and \(t_{0}(p)\approx 8.27071561\) (b) \(p=10\) and \(t_{0}(p)\approx 110.9025198\)

Full size image

Conjecture 1

The equilibrium point \({\bar{x}=\frac{1}{2} (\sqrt{4 p+1}+1 )}\) of Eq. (3) is globally asymptotically stable if \(0< p<2\).

Neimark–Sacker bifurcation

In this section we discuss the existence of Neimark–Sacker bifurcation (for more details see [15–19]) for the unique positive equilibrium and compute asymptotic approximation of the invariant curve near the positive equilibrium point of Eq. (3), according to the procedure given in [16].

If we make a change of variable \(y_{n}=x_{n}-\bar{x,}\) then the transformed equation is given by

$$ y_{n+1}=1+p\frac{y_{n}+\bar{x}}{(y_{n-1}+\bar{x})^{2}}-\bar{x},\quad n=0,1, \dots $$

(17)

By using the substitution \(u_{n}=y_{n-1}\) and \(v_{n}=y_{n}\), we write Eq. (3) in the equivalent form:

$$ \textstyle\begin{cases} u_{n+1} = v_{n}, \\ v_{n+1} = 1+p \frac{v_{n}+\bar{x}}{(u_{n}+\bar{x})^{2}}-\bar{x}. \end{cases} $$

(18)

Let F be the corresponding map defined by

\mathbf{\text{F}} \left(\begin{array}{c}u\\ v\end{array}\right) = \left(\begin{array}{c}v\\ 1+p\frac{v+\overline{x}}{{(u+\overline{x})}^2}-\overline{x}\end{array}\right) .

(19)

It is easy to see that

\mathbf{\text{F}} \left(\begin{array}{c}u\\ v\end{array}\right) = J_{\mathbf{\text{F}}} ( 0 , 0 ) \left(\begin{array}{c}u\\ v\end{array}\right) + \mathbf{\text{G}} \left(\begin{array}{c}u\\ v\end{array}\right) ,

(20)

where

\mathbf{\text{G}} \left(\begin{array}{c}u\\ v\end{array}\right) = \left(\begin{array}{c}0\\ 1+p\frac{v+\overline{x}}{{(u+\overline{x})}^2}+\frac{2pu}{{\overline{x}}^2}-\frac{pv}{{\overline{x}}^2}-\overline{x}\end{array}\right) .

To study Neimark–Sacker bifurcation, we need the following lemma.

Lemma 10

If \(p=p_{0}=2\) then eigenvalues of Jacobian matrix of F at \((0,0)\) are μ and μ̅ where

$$ \mu =\frac{1}{4} (1+i \sqrt{15} ). $$

Moreover, μ satisfies the following:

1. (a)

   \(\mu ^{k}\neq 1\) for \(k=1,2,3,4\).

2. (b)

   \(d= \frac{d|\mu (p)|}{dp} \vert _{p=p_{0}}= \frac{1}{12}>0\).

3. (c)

   Eigenvectors associated to μ are

   $$ \mathbf{q}= \biggl(\frac{1}{4} (1-i \sqrt{15} ),1 \biggr) ^{T}\quad \textit{and}\quad \textbf{p}= \biggl(\frac{2 (\sqrt{15}+i )}{ \sqrt{15}-15 i}, \frac{8}{15+i \sqrt{15}} \biggr) $$

   such that \(\textbf{A}\textbf{q}=\mu \textbf{q}\), \(\textbf{p} \textbf{A}=\mu \textbf{p}\), and \(\textbf{p}\textbf{q}=1\).

Proof

The Jacobian matrix of F is given by

J_{\mathbf{\text{F}}} ( u , v ) = \left(\begin{array}{cc}0& 1\\ -\frac{2p(v+\overline{x})}{{(u+\overline{x})}^3}& \frac{p}{{(u+\overline{x})}^2}\end{array}\right) .

(21)

The eigenvalues of (21)) are \(\mu _{\pm }(p)\) where

$$ \mu _{\pm }(p)=\frac{p \pm \sqrt{p (p -8 \bar{x}^{2} )}}{2 \bar{x}^{2}}. $$

(22)

At \((0,0)\), \(\operatorname{Jac}_{\textbf{F}}(u,v)\) has the form

{Jac}_{\mathbf{\text{F}}} ( 0 , 0 ) = \left(\begin{array}{cc}0& 1\\ -\frac{2p}{{\overline{x}}^2}& \frac{p}{{\overline{x}}^2}\end{array}\right) .

(23)

For \(p=p_{0}=2\), it is easy to see that \(\bar{x}=2\) and

The eigenvalues of A are μ and μ̅ where

$$ \mu =\frac{1}{4} (1+i \sqrt{15} ). $$

The eigenvectors corresponding to μ and μ̅ are q and \(\overline{\textbf{q}}\) where

$$ \mathbf{q}= \biggl(\frac{1}{4} (1-i \sqrt{15} ),1 \biggr) ^{T}. $$

One can prove that \(|\mu |=1\), \(\mu ^{2}=-\frac{7}{8}+i\frac{\sqrt{15}}{8}\), \(\mu ^{3}=- \frac{11}{16}-i\frac{3 \sqrt{15}}{16}\), \(\mu ^{4}=\frac{17}{32}-i\frac{7 \sqrt{15}}{32}\), from which follows that \(\mu ^{k}\neq 1\) for \(k=1,2,3,4\).

From (22) we have

$$ \bigl\vert \mu (p) \bigr\vert ^{2}=\mu (p) \overline{\mu (p)}=\frac{2 p }{\bar{x}^{2}}=\frac{8 p}{ (\sqrt{4 p+1}+1 )^{2}}, $$

from which we get

$$ \frac{d}{dp} \bigl\vert \mu (p) \bigr\vert = \frac{\sqrt{2}}{\sqrt{p (4 p+1)} (\sqrt{4 p+1}+1 )}, $$

which, by substituting \(p_{0}=2\), simplifies to

$$ \frac{d \vert \mu (p)\vert }{dp}\bigg|_{p=p_{0}}= \frac{1}{12}>0. $$

It is easy to see that \(\textbf{p}\textbf{A}=\mu \textbf{p}\) and \(\textbf{p}\textbf{q}=1\). □

Theorem 6

Let

$$ {x_{n+1}=1+p\frac{x_{n}}{x^{2}_{n-1}}}. $$

Assume that \(p=p_{0}=2\). Then there exists a neighborhood \(\mathcal{O}\) of the equilibrium point \((\bar{x},\bar{x})=(2,2)\) and sufficiently small parameter \(\delta >0\) such that if \(|p-2|<\delta \) and \(x_{0}, x_{-1}\in O\mathcal{}\), then ω-limit set of solutions of Eq. (3), with initial condition \(x_{0}\), \(x _{-1}\) is \((\bar{x},\bar{x})\) if \(-\delta < p-2<0\) and belongs to a closed invariant \(C^{1}\) curve \(\varGamma (p)\) encircling the equilibrium point \((\bar{x},\bar{x})\) if \(0< p-2<\delta \). Furthermore, \(\varGamma (2)= \{(2,2)\}\) and invariant curve \(\varGamma (p)\) can be approximated by

\begin{array}{rcl}\left(\begin{array}{c}u\\ v\end{array}\right)& \approx & \left(\begin{array}{c}\overline{x}\\ \overline{x}\end{array}\right)\\ & & +\left(\begin{array}{c}\frac{1}{144}(72\sqrt{p-2}(\sqrt{15}sin(\theta )+cos(\theta ))+(p-2)(9\sqrt{15}sin(2\theta )-95cos(2\theta )+120))\\ \frac{1}{36}(72\sqrt{p-2}cos(\theta )+(p-2)(\sqrt{15}sin(2\theta )+25cos(2\theta )+30))\end{array}\right),\end{array}

where \(\theta \in \mathbb{R}\).

Proof

Let \(p=p_{0}+\delta \) where δ is a sufficiently small parameter. From Lemma 10 we can transform (18) into the normal form

$$ z_{n+1}=\mu (\delta )z_{n}+c(\delta )z_{n}^{2} \bar{z}_{n}+O\bigl( \vert z_{n} \vert ^{4} \bigr). $$

In the polar coordinates it can be written as

\left(\begin{array}{c}{r}_{n+1}\\ {\theta }_{n+1}\end{array}\right) = \left(\begin{array}{c}|\mu (\delta )|r_n+a(\delta )r_n^3+O(r_n^4)\\ {\theta }_n+\text{arg}\mu (\delta )+b(\delta )r_n^2+O(r_n^3)\end{array}\right) ,

(24)

where \(a(\delta )=\operatorname{Re}(c(\delta )/\mu (\delta ))\) and \(b(\delta )=\operatorname{Im}(c(\delta )/\mu (\delta ))\). Performing a Taylor expansion of the coefficients of the first equation of (24) about \(\delta =0\), we have

$$ r_{n+1}=(1+d\delta )r_{n}+a(0) r_{n}^{3}+O \bigl(r_{n}^{4}\bigr). $$

Now, we compute \(a(0)\) using the following procedure from [16]. First, we compute \(\mathbf{K}_{20}\), \(\mathbf{K}_{11}\) and \(\mathbf{K}_{0,2}\) defined in [16]. Substituting \(p=p_{0}\) and x̄ into (20), we get

{\mathbf{\text{F}}}_0 \left(\begin{array}{c}u\\ v\end{array}\right) = A \left(\begin{array}{c}u\\ v\end{array}\right) + {\mathbf{\text{G}}}_0 \left(\begin{array}{c}u\\ v\end{array}\right) ,

(25)

where

{\mathbf{\text{G}}}_0 \left(\begin{array}{c}u\\ v\end{array}\right) = \left(\begin{array}{c}0\\ \frac{2(v+2)}{{(u+2)}^2}+u-\frac{v}{2}-1\end{array}\right) .

Hence, for \(p=p_{0}\) system (18) is equivalent to

\left(\begin{array}{c}{u}_{n+1}\\ v_{n+1}\end{array}\right) = \mathbf{A} \left(\begin{array}{c}{u}_n\\ v_n\end{array}\right) + {\mathbf{\text{G}}}_0 \left(\begin{array}{c}{u}_n\\ v_n\end{array}\right) .

(26)

Define the basis of \(\mathbb{R}^{2}\) by \(\boldsymbol{\varPhi }=( \textbf{q},\bar{\textbf{q}})\), then we can represent \((u,v)\) as

\left(\begin{array}{c}u\\ v\end{array}\right) = \mathit{\Phi } \left(\begin{array}{c}z\\ \overline{z}\end{array}\right) = ( \mathbf{\text{q}} z + \overline{\mathbf{\text{q}}} \overline{z} ) = \left(\begin{array}{c}\frac{1}{4}(1-i\sqrt{15})z+\frac{1}{4}(1+i\sqrt{15})\overline{z}\\ \overline{z}+z\end{array}\right) .

By using this, we have

\begin{array}{c}\mathbf{\text{G}}\left(\mathit{\Phi }\left(\begin{array}{c}z\\ \overline{z}\end{array}\right)\right)\hfill \\ =\left(\begin{array}{c}0\\ \frac{1}{4}(-2(\overline{z}+z)+(1+i\sqrt{15})\overline{z}-\frac{128(\overline{z}+z+2)}{{(-(\sqrt{15}-i)\overline{z}+(\sqrt{15}+i)z+8i)}^2}-i\sqrt{15}z+z-4)\end{array}\right).\hfill \end{array}

(27)

Let

\mathbf{G} \left(\mathit{\Phi }\left(\begin{array}{c}z\\ \overline{z}\end{array}\right)\right) = \frac{1}{2} ({\mathbf{g}}_{20}{z}^2+2{\mathbf{g}}_{11}z\overline{z}+{\mathbf{g}}_{02}{\overline{z}}^2) + O (|z{|}^3) .

Then, we have

\begin{array}{rl}{\mathbf{g}}_{20}& =\frac{{\partial }^2}{\partial z^2}\mathbf{\text{G}}\left(\mathit{\Phi }\left(\begin{array}{c}z\\ \overline{z}\end{array}\right)\right){|}_{z=0}=\left(\begin{array}{c}0\\ -\frac{25-i\sqrt{15}}{16}\end{array}\right),\\ {\mathbf{g}}_{11}& =\frac{{\partial }^2}{\partial z\partial \overline{z}}\mathbf{\text{G}}\left(\mathit{\Phi }\left(\begin{array}{c}z\\ \overline{z}\end{array}\right)\right){|}_{z=0}=\left(\begin{array}{c}0\\ \frac{5}{4}\end{array}\right),\\ {\mathbf{g}}_{02}& =\frac{{\partial }^2}{\partial {\overline{z}}^2}\mathbf{\text{G}}\left(\mathit{\Phi }\left(\begin{array}{c}z\\ \overline{z}\end{array}\right)\right){|}_{z=0}=\left(\begin{array}{c}0\\ -\frac{25+i\sqrt{15}}{16}\end{array}\right).\end{array}

(28)

Let

\begin{array}{rl}{\mathbf{K}}_{20}& ={({\mu }^{2}I-A)}^{-1}{\mathbf{g}}_{20}=\left(\begin{array}{c}-\frac{95+9i\sqrt{15}}{144}\\ \frac{25-i\sqrt{15}}{36}\end{array}\right),\\ {\mathbf{K}}_{11}& ={(I-A)}^{-1}{\mathbf{g}}_{11}=\left(\begin{array}{c}\frac{5}{6}\\ \frac{5}{6}\end{array}\right),\\ {\mathbf{K}}_{02}& ={({\overline{\mu }}^{2}I-A)}^{-1}{\mathbf{g}}_{02}={\bar{K}}_{20},\end{array}

(29)

and

\begin{array}{c}\mathbf{G}(\mathit{\Phi }\left(\begin{array}{c}z\\ \overline{z}\end{array}\right)+\frac{1}{2}({\mathbf{K}}_{20}{z}^2+2{\mathbf{K}}_{11}z\overline{z}+{\mathbf{K}}_{02}{\overline{z}}^2))\hfill \\ =\frac{1}{2}({\mathbf{g}}_{20}{z}^2+2{\mathbf{g}}_{11}z\overline{z}+{\mathbf{g}}_{02}{\overline{z}}^2)\hfill \\ +\frac{1}{6}({\mathbf{g}}_{30}{z}^3+3{\mathbf{g}}_{21}{z}^2\overline{z}+3{\mathbf{g}}_{12}z{\overline{z}}^2+{\mathbf{g}}_{03}{\overline{z}}^3)+O(|z{|}^4).\hfill \end{array}

(30)

Then, we have

\begin{array}{rcl}{\mathbf{g}}_{21}& =& \frac{{\partial }^3}{\partial z^2\partial \overline{z}}\mathbf{\text{G}}(\mathit{\Phi }\left(\begin{array}{c}z\\ \overline{z}\end{array}\right)+\frac{1}{2}{\mathbf{K}}_{20}{z}^2+{\mathbf{K}}_{11}z\overline{z}+\frac{1}{2}{\mathbf{K}}_{02}{\overline{z}}^2){|}_{z=0}\\ & =& \left(\begin{array}{c}0\\ -\frac{1+3i\sqrt{15}}{36}\end{array}\right).\end{array}

(31)

Consequently,

$$\begin{aligned} a(0) =&\operatorname{Re} \biggl(\frac{c(0)}{\mu } \biggr) \\ =& \frac{1}{2} \operatorname{Re}(\textbf{p}\mathbf{g}_{21}\bar{ \mu })=-\frac{1}{12}< 0. \end{aligned}$$

(32)

By Lemma 10, we know that

$$ d=\frac{d \vert \mu (\delta ) \vert }{d\delta }\bigg|_{\delta =0}=\frac{d \vert \mu (p)\vert }{dp}\bigg|_{p=p_{0}}= \frac{1}{12}>0. $$

By the result in [16], we have an asymptotic approximation of the invariant curve as

\left(\begin{array}{c}u\\ v\end{array}\right) \approx \left(\begin{array}{c}\overline{x}\\ \overline{x}\end{array}\right) + 2 {\rho }_0 Re \left(\mathbf{q}{e}^{i\theta }\right) + {\rho }_0^2 (Re\left({\mathbf{K}}_{20}{e}^{2i\theta }\right)+{\mathbf{K}}_{11}) ,

where

$$\begin{aligned} d =&\frac{d}{dp} \bigl\vert \mu (p)\bigl\vert \bigg|_{p=2},\\ \rho _{0} =&\sqrt{- \frac{d}{a(0)}\delta },\quad \theta \in \mathbb{R}. \end{aligned}$$

Since \(\rho _{0}=\sqrt{p-2}\) for \(0< p-2<\delta \), where \(\delta >0\) is a sufficiently small parameter, from the previous calculation we have

\begin{array}{rcl}\left(\begin{array}{c}u\\ v\end{array}\right)& \approx & \left(\begin{array}{c}\overline{x}\\ \overline{x}\end{array}\right)\\ & & +\left(\begin{array}{c}\frac{1}{144}(72\sqrt{p-2}(\sqrt{15}sin(\theta )+cos(\theta ))+(p-2)(9\sqrt{15}sin(2\theta )-95cos(2\theta )+120))\\ \frac{1}{36}(72\sqrt{p-2}cos(\theta )+(p-2)(\sqrt{15}sin(2\theta )+25cos(2\theta )+30))\end{array}\right).\end{array}

This completes the proof. □

Conclusion

In this paper, we investigated the stability of the following second-order rational difference equation, \(x_{n+1}=1+px_{n}/x_{n-1} ^{2}\), \(n=0,1,\ldots \) , with positive initial conditions and \(p>0\). We showed that the parameter space splits into three regions: \(p<2\), \(p=2\), and \(p>2\). We proved a global stability result for \(p\leq (1+\sqrt{2})/2\). Based on our numerical computations, we conjectured that the unique positive equilibrium is globally asymptotically stable for \(0< p<2\). We proved boundedness of all solutions. In the case \(1< p<+\infty \), to prove the existence of a sequence of invariant and attractive sets that contain all solutions, we constructed compact sets \(\mathcal{S}_{t}\) which are invariant for all t such that \(t_{0}(p)\leq t<+\infty \) for some \(t_{0}(p)> \bar{x}\). In the case \(p=2\), we studied Neimark–Sacker bifurcations for the positive equilibrium point. Also, we computed the approximation of the invariant curve near the positive equilibrium point. The positive equilibrium point is a repeller for \(p>2\). By numerical computations, we confirmed our analytic results. See Figs. 3 and 4.

Figure 3

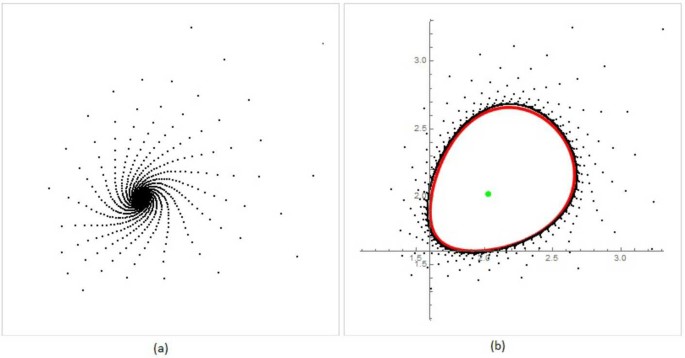
(a) Trajectory (black) for \(p=1.99\). (b) Trajectory (black) and asymptotic approximated invariant curve (red) for \(p=2.01\)

Full size image

Figure 4

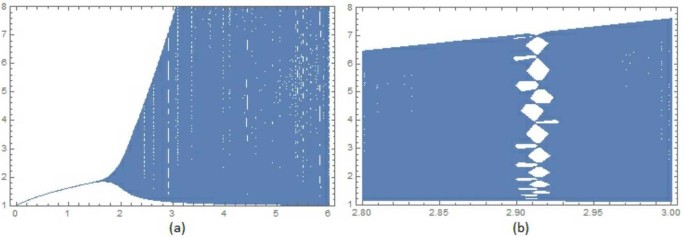
Bifurcation diagrams in the p–x plane

Full size image

References

1. 1.

   Kulenović, M.R.S., Ladas, G.: Dynamics of Second Order Rational Difference Equations, with Open Problems and Conjectures. Chapman & Hall, London (2001)

   Book  Google Scholar

2. 2.

   Khyat, T., Kulenović, M.R.S., Pilav, E.: The Naimarck–Sacker bifurcation of a certain difference equation. J. Computational Analysis and Applications. 23(8) (2017)

3. 3.

   El-Morshedy, H.A.: The global attractivity of difference equations of nonincreasing nonlinearities with applications. Comput. Math. Appl. 45, 749–758 (2003)

   MathSciNet  Article  Google Scholar

4. 4.

   Kulenović, M.R.S., Merino, O.: Global attractivity of the equilibrium of \(x_{n+1}=\frac{px_{n}+x_{n-1}}{qx_{n}+x_{n-1}}\) for \(q< p\). J. Differ. Equ. Appl. 12, 101–108 (2006)

   Article  Google Scholar

5. 5.

   Kulenović, M.R.S., Merino, O.: Stability analysis of Pielou's equation with period-two coefficient. J. Differ. Equ. Appl. 13, 383–406 (2007)

   MathSciNet  Article  Google Scholar

6. 6.

   Krause, U.: Positive Dynamical Systems in Discrete Time. Theory, Models, and Applications. De Gruyter Studies in Mathematics, vol. 62. de Gruyter, Berlin (2015)

   Book  Google Scholar

7. 7.

   McArdle, D., Merino, O.: Global dynamics of Leslie host-parasite model. J. Differ. Equ. Appl. 24(1), 82–106 (2017). https://doi.org/10.1080/10236198.2017.1397139

   MathSciNet  Article  MATH  Google Scholar

8. 8.

   Kulenović, M.R.S., Merino, O.: A global attractivity result for maps with invariant boxes. Discrete Contin. Dyn. Syst., Ser. B 6, 97–110 (2006)

   MathSciNet  MATH  Google Scholar

9. 9.

   Kocic, V.L., Ladas, G.: Global Behavior of Nonlinear Difference Equations of Higher Order with Applications. Kluwer Academic, Norwell (1993)

   Book  Google Scholar

10. 10.

    Kulenović, M.R.S., Ladas, G., Sizer, W.S.: On the recursive sequence \(x_{n+1}=\frac{\alpha x_{n}+\beta x_{n-1}}{\gamma x_{n}+Cx_{n-1}}\). Math. Sci. Res. Hot-Line 2(5), 1–16 (1998)

    MathSciNet  MATH  Google Scholar

11. 11.

    Smith, H.L.: Planar competitive and cooperative difference equations. J. Differ. Equ. Appl. 3, 335–357 (1998)

    MathSciNet  Article  Google Scholar

12. 12.

    Janson, S.: Resultant and discriminant of polynomials (2010). http://www2.math.uu.se/~svante/papers/sjN5.pdf. Accessed 20 June 2019

13. 13.

    Kirwan, F.: Complex Algebraic Curves. London Mathematical Society Student Texts. Cambridge University Press, Cambridge (1992)

    Book  Google Scholar

14. 14.

    Yang, L., Hou, X., Zeng, Z.: Complete discrimination system for polynomials. Sci. China Ser. E 39(6), 628–646 (1996)

    MathSciNet  MATH  Google Scholar

15. 15.

    Hale, J.K., Kocak, H.: Dynamics and Bifurcations. Texts in Applied Mathematics, vol. 3. Springer, New York (1991)

    Book  Google Scholar

16. 16.

    Murakami, K.: The invariant curve caused by Naimark–Sacker bufurcation. Dyn. Contin. Discrete Impuls. Syst. 9(1), 121–132 (2002)

    MathSciNet  MATH  Google Scholar

17. 17.

    Robinson, C.: Stability, Symbolic Dynamics, and Chaos. CRC Press, Boca Raton (1995)

    MATH  Google Scholar

18. 18.

    Wan, Y.H.: Computation of the stability condition for the Hopf bifurcation of diffeomorphisms on \(\mathbb{R}^{2}\). SIAM J. Appl. Math. 34(1), 167–175 (1978)

    MathSciNet  Article  Google Scholar

19. 19.

    Wiggins, S.: Introduction to Applied Nonlinear Dynamical Systems and Chaos, 2nd edn. Texts in Applied Mathematics, vol. 2. Springer, New York (2003)

    MATH  Google Scholar

Download references

Acknowledgements

The authors are thankful to the anonymous referees for their helpful comments and the editor for constructive suggestions to improve the paper in current form.

Availability of data and materials

Not applicable.

Author information

Affiliations

1. Department of Mathematics, University of Sarajevo, Sarajevo, Bosnia and Herzegovina

   Emin Bešo, Senada Kalabušić & Esmir Pilav

2. Faculty of Electrical Engineering, University of Sarajevo, Sarajevo, Bosnia and Herzegovina

   Naida Mujić

Contributions

All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Senada Kalabušić.

Ethics declarations

Ethics approval and consent to participate

Not applicable.

Competing interests

The authors declare that they have no competing interests.

Consent for publication

All authors read and approved the final manuscript.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and Permissions

About this article

Cite this article

Bešo, E., Kalabušić, S., Mujić, N. et al. Boundedness of solutions and stability of certain second-order difference equation with quadratic term. Adv Differ Equ 2020, 19 (2020). https://doi.org/10.1186/s13662-019-2490-9

Download citation

• Received: 23 September 2019

• Accepted: 30 December 2019

• Published: 09 January 2020

• DOI : https://doi.org/10.1186/s13662-019-2490-9

Keywords

• Difference equation
• Birkhoff normal form
• Boundedness
• Invariant set
• Neimark–Sacker bifurcation
• Stability

Finding Points in a Period-2 Solution of a Difference Equation

Source: https://advancesindifferenceequations.springeropen.com/articles/10.1186/s13662-019-2490-9

Share :