Find All Solutions to the Equation 2sinî¸20

Here is a history of questions and answers processed by "Ask the Physicist!". If you like my answer, please consider making a donation to help support this service.

If there is a link to a previously answered question, be patient. Since the files containing the older answers are rather large, it takes some time (maybe as much as 15 seconds or so) to find the appropriate bookmark.

QUESTION:
In lifting an object to a higher level directly over its original location, the energy I expend increases potential energy. But, does some of the energy used in lifting it also go to accelerating it to higher rotational velocities as the circumference of its "orbit" increases as it is raised over its original position? Does this add kinetic energy and mass to the object whereas increasing potential energy does not?

ANSWER:
(Preface: all my calculations below assume that the height lifted is much smaller than the radius of the earth. I also neglect the change in the gravitational force over the distance the mass is lifted. Also, to simplify things, all my calculations are at the equator.) Yes, work is done to increase the kinetic energy. As viewed from an inertial frame, watching the mass M get lifted to h, I estimate that the kinetic energy changes by ΔK≈2hK _initial/R=MhRω ² where R=6.4x10⁶ m is the radius of the earth and ω=7.3x10^-5 s^-1 is the angular velocity of the earth. For example, lifting 1 kg a height of 1 m requires 0.03 J of work to increase the kinetic energy. But wait a minute! Once we acknowledge that the earth is rotating, we have to recognize that the mass, being in a circular orbit, has a centripetal acceleration a _c=Rω ² and therefore the net force on M is Mg-MRω ². Therefore, the net work done is W≈(Mg-MRω ²)h+MhRω ²=Mgh.

QUESTION:
How is the gravitational force directly proportional to the product of masses and inversely proportional to square of distance between the masses? i just want to know how they proven it ?

ANSWER:
It is simply an experimental fact. This hypothesis describes the motion of the bodies in the solar system almost perfectly.

QUESTION:
What factors affect light intensity and how?

ANSWER:
I guess you want a definition of intensity. It is simply the amount of energy passing through an area per second divided by the area. Physicists prefer to measure this as watts per square meter, W/m². But, to discover how convoluted the measurement of intensity can be, see an earlier answser.

QUESTION:
Why don't oranges being carried in a semi-truck get crushed by all the oranges on top?

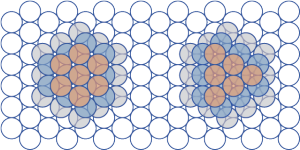
four layers are shown

ANSWER:
It is because of the way that spheres tend to pack together. As you can see by carefully examining the figures above, each orange is pushed down by three oranges from above, is pushed up by three forces from oranges below, and is pushed horizontally by six oranges in the same layer. These twelve forces all are directed toward the center of the orange and all add up to zero net force, but there is a net pressure over the surface of each orange approximately trying to squeeze it into a smaller orange. But an orange is mostly water which is nearly incompressible so the orange does not get crushed. Think of a nicely packed snow ball: if you try to crush it into a smaller ball by squeezing with cupped hands you will fail; to crush it you will have to flatten it by pushing it with diametrically opposed hands. You might think the bottom-most layer would get crushed because there is just one force pushing up; but, each orange has six others in the same layer pushing toward its center and these keep it from getting flattened.

Here is a little more about sphere packing. There are two possible packings which achieve the maximum density of π/(2√3)≈74%: hexagonal close-packed (HCP) face-centered cubic (FCC); these are compared in the figure above (HCP on the left).

FOLLOWUP QUESTION:
What would happen to the oranges once the force exerted upon them reached a critical strength which they couldn't bear? Does the entire group of oranges burst simultaneously in a flood of juice?

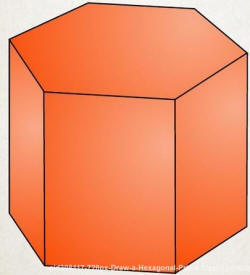
ANSWER:
Because the forces are not spread uniformly over the surface area, there would be a tendency to be squeezed to a different shape but still approximately preserving the volume of each orange. And I would not expect it to happen all at once because the oranges on the bottom are certainly experiencing greater forces. I would expect the out-of-layer forces (from above and below) to tend to flatten the lower-layer oranges but the neighbors in the same layer to cause the oranges to have a hexagonal shape, so the oranges would tend toward a hexagonal-prism shape. Each orange would occupy about the same volume, but the amount of empty space (previously 26%) would decrease and each layer would get thinner. This ignores the possibility of orange peels rupturing, but I would think things would tend toward this shift before much juice flowed!

QUESTION:
What is the effect of mass on torque? A wind turbine fan's blades are commonly very long to increase torque and to decrease speed. How can I decrease speed using MASS? Or, can I increase torque, by increasing of mass, without increasing length of the blade? (without losing the energy.) What is the formula applicable here?

ANSWER:
You are asking many questions here with no simple answers.

The simplest place to start is your first question: does the mass of the rotor have an effect on the torque on it? Typically, the turbine has three blades. I will just analyze a single one and the same arguments could be made for the other two. Call the length of the blade L and assume that the force on it due to the wind is approximately uniform along the length of the blade (the force on a tiny piece of the blade near the center is the same as the force on an identical tiny piece near the end). Then the total force F due to the wind will depend on the length of the blade, but the force per unit length, Φ=F/L will be more useful because it will depend only on how hard the wind is blowing. It is now pretty easy to show that the torque due to the wind is τ _wind=½ΦL ² . So, the answer to your question is no, mass does not affect the torque; the torque depends only on how hard the wind is blowing and how long the blade is.

Your second question is how can you decrease speed by changing the mass M. If I model the blade as a uniform thin stick of length L, its moment of inertia is I=ML ²/3. If it has an angular velocity ω ₁, its angular momentum is L ₁=Iω ₁=Mω ₁ L ²/3. If you increase the mass to M+m, the moment of inertia will increase to I'=(M+m)L ²/3 and its angular velocity will change to ω ₂. But, the angular momentum will not be changed, Iω ₁ =I'ω ₂; you can then solve this for the new angular velocity, ω ₂=(I/I')ω ₁=[M/(M+m)]ω ₁ which is smaller. However, the rotational kinetic energy E of the blade is now lower, E ₁=½Iω ₁ ² and E ₂=½I'ω ₂ ²=½I{(M+m)/M}{[M/(M+m)]ω ₁}²or E ₂=[M/(M+m)]E ₁. On the other hand, if you wanted to add mass but keep the energy the same, E ₂/E ₁=1=I'ω ₂ ²/Iω ₁ ² or ω ₂=ω ₁√[M/(M+m)]; in this case, the angular momentum will have changed.

Your third question is moot since we have established that torque does not depend on mass.

QUESTION:
If I stood beside a small operating hovercraft with a sail built into the front of it and blew air into the sail with a leaf blower I know that the craft would move forward. Now the question.If I sat down on the hovercraft with the leaf blower in hand and we became one with the hovercraft and I then blew air into the sail would we move forward or would action and reaction of the leaf blower neutralize the forward motion?

ANSWER:
It is easiest to understand if you think first of using a stick instead of a leaf blower. Standing on the ground and pushing with the stick on the sail, there is an unbalanced force acting on your hovercraft (the stick). Now, if you stand on the hovercraft, the stick exerts a backward force on you (part of the hovercraft, now) and the stick exerts a forward force on the hovercraft and these cancel out. Or, if you like, the only forces which have any effect on a system are external forces and by becoming part of the system what you do is no longer an external force. The leaf blower is a little trickier, but I believe even worse! The leaf blower will exert a backward force on you (like a little jet engine) and the stream of air will exert a forward force on the sail; but some of the force from the stream of air will be diminished by the air slowing down on its way to sail because of interaction with the still air. So, the net effect would be for the whole hovercraft to move backwards; probably not noticible because of friction and the smallness of the loss of power due to the still air.

QUESTION:
Helium. Where do we get it from if it is lighter than air and doesn't react with any other elements in the normal human tolerant environment?

ANSWER:
Good question. Even though it is the second most abundant element in the known universe, there is virtually none in the atmosphere (because it is so light that its average speed is greater than escape velocity and it shoots off into space) and is not tied up in rocks, water, or other chemicals (because it is inert) like hydrogen is, for example. This element was not even discovered until 1868 as a spectral line in the sun (where untold zillions of tons are being produced every second from nuclear fusion) and not found on earth until 1895 when trace amounts were found coming from uranium ore; the source was as a nuclear decay product in α-decay. The first large amounts were discovered in 1903 as a byproduct mixed with the methane in natural gas wells; today large scale amounts come only from helium trapped underground.

QUESTION:
Why nucleon number is the sum of the number of protons and neutrons instead of the sum of the number of electrons and neutrons or between the number of protons and electrons , explain the logic ?

ANSWER:
It is very simple. Nucleon means either proton or neutron; a proton is a nucleon and a neutron is a nucleon. Nucleon number means number of nucleons. Electrons are not nucleons.

QUESTION:
If basketball (A) weighs 1 lb and is tossed upward to goal (A) at a height of 8 ft (5 ft above my daughter's head) and basketball B is 6lbs, At what height should goal (B) be to generate the same force to toss?

FOLLOWUP QUESTION :
Actually this is not homework, let me explain the situation. My daughter is 5 years old and playing Kindergarten basketball. Only one person on her team can toss the ball high enough to score, the ball weighs roughly 1 lb and the goal is roughly 8 ft high. I purchased a weight trainer ball that is exactly the same diameter as the regulation ball she uses but it's a 6 lb ball. My theory is that I can build her a goal in the house that is not as tall but would require the same energy to make the basket. therefore making her stronger. And when it comes time to shoot the lighter ball in the taller goal, she shouldn't have any problems.

ANSWER:
For the 1 lb ball, the energy which must be supplied is 1x5=5 ft·lb, assumning that she releases the ball at the level of the top of her head. The 6 lb ball, if sent vertically with an energy input of 5 ft·lb, will rise to a height of h=5/6=0.83 ft=10 inches above her head. All this assumes that the ball is thrown straight up. Note that I have not really answered your question because you asked for force and the energy input depends both on force F and the distance s over which it is applied. The energy input W could be written as W=Fs, So, if you assume that she throws it the same way and pushes as hard as she can, the force need not be known.

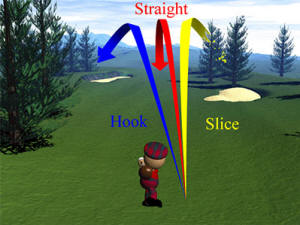
QUESTION:
I am curious about a topic. In golf, if I hit a ball very hard and then I hit one very softly, is the one hit very softly more likely to move or sway in its straight path?

ANSWER:
You refer to "its straight path". No golf ball goes in a straight path, so I presume you mean that it does not curve left or right; such a ball, if not curving, would have a projected path on the ground (like the path of its shadow) which is straight. For a right-handed golfer, a ball which curves right is called a slice and one which curves to the left is called a hook; these have opposite spins. Neglecting the possibility of wind, the reason that a ball curves is because it has spin. But now it gets complicated because:

the hard-hit ball is in the air much longer than the softly-hit ball;
the lateral force causing the curve depends on both the rate of spin and the speed of the ball, so the hard-hit ball will experience more lateral force than the softly-hit one if they have the same spin;
even if the slow ball has a bigger lateral force, the fast ball is likely to be deflected a greater distance because of its longer flight time;
a lateral wind will exert the same force on both, but the fast ball will be deflected farther because of the longer time.

So, you see, there is no simple answer. To avoid curving, learn to hit the ball without imparting significant spin!

QUESTION:
We had a phenomenon happen recently about 8:30 PM that is inexplicable to us, but there must be some explanation. My wife & I were in separate rooms when we both heard an extremely loud noise from the living room! The noise sounded like a large glass that just hit a hard tile floor, but loudness was magnified. As it turned out we came into the living room to find a glass platter that we had sitting on the coffee table for about a year just shattered. –It broke completely by itself as there was no one in the room. Do you know how this may have shattered/blew apart all by itself?We used the platter to put 3 little oil lamps on. Inside our house the next morning at 6 AM we heard thunder outside so thought it might have had something to do with the barometric pressure.Very low barometric pressure & the type of glass it was made up combined just right to explode it like that? The temperature was a constant 68 degrees as it was for the months that was on the table. If you have any idea about this, we would appreciate it.

ANSWER:
Glass, as you know, is manufactured at very high temperatures. It has a quite large coefficient of theremal expansion (a large change in size for a small change in temperature) and is a poor conductor of heat. This means that as it cools it does not all cool at the same time. This can result in very large stresses being "frozen in" at some locations. What causes it to spontaneously break is usually difficult to determine; most likely it had recently been bumped or your oil lamps might have caused hot spots on the glass. Such things could have caused a tiny fracture to begin and the final shattering could easily come at some unpredictable later time. Unusual but not unexpected.

QUESTION:
On a skate board going down a .5 mile hill at 45 degrees slopes if I weigh 187 lbs how many mph would I be going by the bottom of the slope.

FOLLOWUP QUESTION:
This isn't homework I'm a 35 year old heavy equipment operator and my son had a accident on skate board and we are curious how fast he was going when he wiped out. I just wasn't sure how accurate I was when I said about 30-35mph. Please if you don't know just tell me so I can find someone who does—we got bets on it now amongst the family.

ANSWER:
Wow, 45º is pretty darn steep! A half mile would correspond to his having dropped by about 0.35 miles≈560 m. If there were no friction at all his speed would have been v=√(2gh)=√(2x9.8x560)=105 m/s=235 mph! Back to the drawing board! There is some friction due to the wheels and bearings and I estimate that this is probably not more than about 15 lb; this would only slow him down to about 99 m/s=220 mph. Back to the drawing board! Finally, since the speed is going to get pretty big, we need to take air drag into consideration because the drag force is proportional to the square of the speed. A rough estimate would be that the force is about F _drag≈¼Av ² where A is the area his body presents to the onrushing wind. When F _drag is equal the net force down the incline (component of weight minus friction, which I estimate to be about 117 lb=520 N), he will stop accelerating. Taking his area to be about 2 m², you can then solve ¼Av ²=520 to get v=32 m/s=70 mph. This is all very rough but should give you an order-of-magnitude estimate. (I still find it hard to believe that he went down a half mile, 45º slope without braking at all!)

QUESTION:
I am curious about generating power in space. Why do they always use solar instead of the windmill type of generation? A coil/magnet rotating. It seems to me, once the rotation is started, it would continue forever? Thus if you used a rocket to start the rotating part of the generator, and it kept spinning, could you use the magnetic field to protect say, an astronaut inside the generator? If it was big enough. Would you get perpetual energy if you used the electricity created in say, a microwave rocket engine or electromagnet. Or does the magnetic force alone cause the spin to lose momentum?

ANSWER:
So, you start something rotating in a vacuum and it never stops because there is no air drag. You could even imagine making extremely low-friction bearings so you could mount this on the side of your spacecraft and it would at least spin for a very long time before slowing down. But, the minute you hook it up to a generator you are asking it for energy so it immediately begins to slow down, giving its kinetic energy to you to power a light bulb, maybe. There is no free lunch in this universe, and if you want energy you need something to give it to you and the sun is the most convenient source in our neighborhood.

QUESTION:
Is dark energy real? If all matter in the universe expanded from a single point the size of an atom (the big bang) wouldn't things be moving faster from each other because of geometry? If you start with a sphere the size of an atom and it expanded outwards over billions years even a Planck length size degree difference would be immense. It would cause things to move farther apart at faster rates as time went on. Are things moving faster away from each other because of geometry and angles, and not from hypothesized dark energy?

ANSWER:
I do not usually answer questions in astronomy/astrophysics/cosmology but think I can answer this one. If a collection of objects interact only via an attractive force (gravity in this case), any one of them can only speed up when moving toward their center of mass. The details of the motion would be determined by the initial conditions. If all the objects were moving away from some common point at some time, the only possible motions would be

for all to move forever away from each other, but forever slowing down;
for all to slow down and eventually turn around and speed up back together; or
for some to come together and some to keep going.

The simple reason is that the potential energy of such a system increases as the objects get farther apart so the kinetic energy must decrease to conserve energy.

QUESTION:
But I read somewhere that the faster you travel through space, the slower you travel through time, and if you reach light speed, time stops. If that's true, why does light have a speed, instead of just being instant? Does time not stop for light when it travels?

ANSWER:
First, you cannot reach light speed, no object with mass can; so let's not talk about how fast your clock would be running if you went light speed. What happens at high speed is that your clock will run slow when measured by an observer you are passing. To you, time would seem perfectly normal; however you would observe distances along your line of travel to be shorter and therefore you would take a shorter time to get there. Now, if you are traveling at almost the speed of light, say 99.99% of it, I would still see you traveling at that speed regardless of what your clock is doing; so, if the photon had a (nonchanging) clock on it, I would still see it going at the speed of light. Regarding whether time stops for a photon, my stock answer is that a photon does not have a "point of view" and it is pointless to ask how fast a photon's clock is moving because a photon does not carry a clock with it.

QUESTION:
Does the existence of gravitational waves imply the existence of gravitons?

ANSWER:
No, gravitational waves have nothing to do with gravitons. Gravitational waves are predicted by general relativity, the best current theory of gravity. Gravitons would be the quanta of the gravitational field is a successful theory of quantum gravity is ever devised. You can look in the faq page for earlier answers about gravitons and general relativity.

QUESTION:
I've been dealing with a false prophet who says that a comet is coming and is going to skim the earth, as if to skip off of it, like a stone skipping on water. Is this even possible? She says it will skip off of the earth and keep going into space. Please let me know if this is even possible?

ANSWER:
Yes, I believe this is indeed possible. You might recall that during the Apollo 13 failed moon mission there was concern that if the spacecraft reentry angle were too small that they would "skip off" the atmosphere into space.

QUESTION:
If it's true that oceanic tides can be caused when the moon's gravity pulls the molecules of ocean water up and away from earth by a certain distance, and if it's also true that earth's atmospheric tides can, likewise, also be caused by the moon's gravity pulling the molecules in the atmosphere up and away from earth by a certain distance, then what stops the atmospheric molecules, once they have accelerated even just a tiny distance in the direction away from earth and towards the moon, from continuing on their journey to the moon? (Let's, for example, say that the atmospheric molecules in question are-to simplify matters-the ones at the very top of earth's atmosphere, so that no other atmospheric molecules are between these particular atmospheric molecules and the moon, as the moon pulls on them.)

ANSWER:
This can get very complicated because the molecules in the air have a whole range of speeds from very slow to very fast, but I do not think that that complication is important to answer your question. The reason that the molecules do not fall to the moon is the same as if you throw a ball straight up and it does not fall to the moon—the earth is pulling on it harder than the moon is. How anything moves is determined by the net force on it and its weight (the force the earth exerts on it) is bigger by far than its "moon weight".

QUESTION:
I need to figure out the force of impact from an object weighing 3.25 lbs falling from 2' I have on reference that a five lb object falling two feet creates a force of impact of approximately 319 lbs. This is not a school question. I got hit in the head with this object.

ANSWER:
I always try to emphasize that you cannot know how much force an object exerts when it hits unless you know how quickly it stops (or, equivalently, how far it goes while stopping). I find that the object was going about 11 ft/s when it hit your head. Suppose that it stopped in about 1 inch; in that case, the average force during the time of stopping would have been about 75 lb. Had it stopped in ½ inch, the force would have been about 150 lb.

QUESTION:
If photons are the charge carriers for the electromagnetic force, then why don't magnets and power lines glow in the dark? Is it because those photons are not in the visible part of the spectrum or is it something else?

ANSWER:
Your terminology is a little off. Photons are the quanta of the electromagnetic field; we then think of them as the "messengers of the force" communicating the force among charged particles. However, they are virtual photons which means that they pop into and out of existence very quickly, too quickly for you to observe them—hence, no glow! Also, if you think about it for a minute, if you saw a glow and the fields did not change, that would violate energy conservation.

QUESTION:
If the planet earth was perfectly smooth and spherical will the water cease to flow?

ANSWER:
Not if everything else stayed the same. If the earth were completely isolated, not rotating, and without atmosphere, water would flow until it formed a uniform layer over the earth; eventually any currents would damp out due to the viscosity of the water. The fact that the earth is rotating and heated by the sun and has an atmosphere would mean that the water would try to distribute itself mostly uniformly but with an equatorial bulge; however heating and cooling of the atmosphere would cause weather patterns and the resulting winds would move the water around just like what happens today. Also, the moon causes tides which are, by definition, motions of the water. You probably could think of many more reasons the water would not become totally static.

QUESTION:
I am trying to figure this out for a dear Uncle on Vancouver Island as a challenge. I have suffered a concussion so trying is difficult. He used to live in S. Wales and dropped stones done old coal shaft. He was a teacher. Wonder if you could help me please: "A stationary rock is allowed to drop down an 800 foot shaft. Without compensating for air resistance, how far does it fall during the sixth second of its descent? This is the formula. Assume gravity value to be 32 feet per second per second. Please set out your answer clearly showing your thought process, line by line. Use words as well as numbers. I'm afraid your answer so far is incorrect. If needed, the formula we used was S = ut + half gt²." Thank you very much. I am in Gr 5!! I want to by a physicist.

ANSWER:
I will assume that this is not a homework problem (forbidden on this site!); at least if it is you went to a lot of trouble to disguise it! Your equation is right except since we will start the clock (t=0) when you let go of the stone, u=0 because u in your equation is the speed at t=0. Also this equation assumes that S=0 at t=0 and that S increases in a downward direction. So, at the end of 5 seconds (the beginning of the 6^th second) the position is S ₅=½x32x5²=400 ft; at the end of 6 seconds the position is S ₆=½x32x6²=576 ft. So the total distance traveled is 176 ft. I trust you will not present this work to your uncle as your own.

QUESTION:
I have a really general question regarding the concept of work in terms of Physics. I'm aware that if work is negative, it means that the displacement and force act in opposite directions. However, does negative work also always imply that the the speed of the object is decreasing, or is this only true when looking at objects moving on a horizontal plane.

ANSWER:
The acceleration of any object is determined by all the forces on it. If only one force acts on an object and the work done is negative, it must be slowing down. If any other forces are present, all bets are off. For example, a box sliding down an incline has friction f doing negative work and gravity mgsinθ doing positive work; if f<mgsinθ the box will be speeding up.

QUESTION:
I'm a physics teacher in South Australia. My question is related to the He-Ne laser and has bothered me for some time as to the actual mechanics. As He is raised to 20.61eV and then transfers to Ne with 20.66eV for population inversion etc... where has the extra 0.05eV appeared from? the quanta of energy is lower therefore Ne electrons should not be excited to that state.

ANSWER:
It comes from the kinetic energy of the collision between the He and Ne.

QUESTION:
Why is water used to cool car engines?

ANSWER:
Because it is cheap, readily available, nontoxic, minimally corrosive, and can be kept from boiling with pressure. Perhaps most important, though, is that it has a high specific heat which means it can absorb a lot of heat without a large temperature increase.

QUESTION:
What would be the estimated terminal velocity be of a 4,300lb car falling from 30,000ft above sea level be?

ANSWER:
The terminal velocity, v _t, does not depend on the altitude from which you drop your car. This can be a very tricky problem because v _t does depend on the density of the air which changes greatly from sea level to 30,000 ft. So to get a first estimate, I will just assume sea level density everywhere. There is an estimate for the drag force in sea level air which is good for a rough estimate, F _D= ¼Av ² where A is the cross sectional area and v is the speed. From this you can show that v _t=2 √( mg/A ). In SI units, m =4300 lb=1950 kg, g =9.8 m/s², and A ≈2x4=8 m² (estimating the car as 2 m wide and 4 m long). Then v _t ≈100 m/s=224 mph.

I guess we should now ask whether we expect it to reach terminal velocity before it hits the ground. Actually, it will technically never really reach terminal velocity, only approach it—see an earlier answer. I will calculate how far it falls before it reaches 99% of v _t. In the earlier answer, I show that the height from which you must drop it for it to reach terminal velocity with no air drag is h ^{no drag}=v _t ²/(2g), and the height from which you drop it for it to reach 99% of terminal velocity with air drag is h ^drag=1.96v _t ²/g (derived from the expression v/v _t=0.99=√[1-exp(-2gh/v _t ²)]. So, for your case, h ^{no drag}≈510 m and h ^drag≈2000 m. At 2000 m (around 6000 ft) the air is about 85% the density of sea-level air, so I believe that my approximation assuming constant density is pretty good and the car would probably reach 99% of the terminal velocity by the time it hit the ground. To actually put in the change in density with altitude would make this a much more difficult problem.

QUESTION:
What is after death (AD), birth of christ (bc)? Then how we are caluclate the age difference in between AD & BC.

ANSWER:
This is not physics, but easily answered. Actually, AD is anno domini, (in the year of the Lord in Latin) and BC is before Christ. The dividing line is, supposedly, either the birth or conception of Jesus. Times before are labeled BC and those after are labeled AD. There is no year zero, so the first year after this time is labeled 1 AD and the first year before is labeled 1 BC. Hence, the time from, e.g., January 1, 10 BC to January 1, 10 AD is 20 years; but, the time from January 1, 1 AD to January 1, 20 AD is 19 years.

QUESTION:
We're trying to design a vessel for working in the vacuum of space. We have a vacuum chamber that can pull a 0.01 atm partial vacuum, so the question is : How does the force difference compare on the walls of a vessel, with 14 psi inside to outside chamber or space, i.e. force comparison between 0.01 atm in the chamber and the 10^-14 in space? My guess is that we are capturing 99% of the effective force differential using the chamber, so not much more to expect from the vacuum of space.

ANSWER:
Ok, the 14 psi inside your chamber is about 0.953 atm and the pressure outside is 0.01 atm making the net pressure difference 0.943 atm. The pressure outside in space is, for all intents and purposes, zero, so the net pressure difference would be 0.953 atm. So, the percent difference is 100x(0.953-0.943)/0.953=1.05%, about what you guessed. In other words, the force on any part of the walls of your chamber is about 1% smaller than it would be in space.

QUESTION:
Not sure if this is physics or not but how can you record silent sound ? I found the patent for it on google it's 5159703 and I wanna know how you can record it because a regular microphone doesn't pick it up.

ANSWER:
The idea here is essentially the same as AM radio where the high-frequency radio wave is modulated by the audible message. For this invention the radio wave is replaced with sound of a frequency larger than is audible but modulated by an audible signal. You could certainly make a detector (call it a microphone if you like) to detect these high-frequency sound waves; ultrasound imaging in medicine does just that. Then you would need some electronics to extract the audible signal from the carrier, just like you need a radio receiver to extract the audible signal from the AM radio carrier.

QUESTION:
Does a round and square object, the same weight, fall the same?

ANSWER:
If air drag is negligible, like if you drop them from a few feet, yes. If they fall fast enough for air drag to be important, they will fall differently and, if they are about the same size, say a sphere and a cube, the sphere will fall faster. That may be all you want, but I will go on and explain in a bit more detail. The drag force F _D on an object may be approximated for every day objects, masses, and speeds as F _D =½C _D ρv ² A where ρ is the density of the air, v is the speed, A is the cross-sectional area presented to the onrushing air, and C _D is called the drag coefficient. C _Ddepends only on the shape of the object. C _D≈0.5 for a sphere and C _D≈0.8 for a cube (falling with one face to the wind). So, if their areas are about the same, the drag on the sphere will be smaller and it will go faster. Of course if the sphere area were ten times bigger than the cube area, that would be more important than the somewhat smaller drag coefficient and the cube would win.

QUESTION:
What would happen if light traveled at normal speed?

ANSWER:
I recommend the Mr Thompkins books by George Gamov.

QUESTION:
Is it correct to say that nuclear fusion violates the law of conservation of mass since a portion of the mass is converted into photons?

ANSWER:
Well, you could say that if there were such a law as conservation of mass. Since 1905 when Albert Einstein showed us that mass is just another form of energy, the only valid such law is conservation of energy. Even in chemistry where conservation of mass appears to be correct, the ultimate source of energy is mass being changed into kinetic energy of the chemical reaction products (heat); chemistry is such an inefficient source of energy that the mass changes are miniscule.

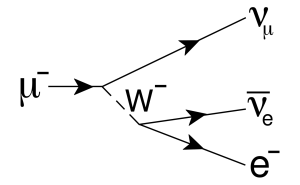
QUESTION:
Can you tell me why muons are extremely unstable (lasting only fractions of a second) while electrons and neutrinos are pretty much stable? I just don't get why muons are so unstable since they're just leptons like electrons and neutrinos just more massive than the other two.

ANSWER:
If you look at the decay of the muon, you will see that the mass of the products, an electron and two neutrinos, is much less than the mass of the muon. This means that the decay is energetically possible, energy is released by the decay so the decay products have kinetic energy afterwards. In nature, almost always when a process is energetically possible it will occur. Only in cases where a decay would be prohibited by some selection rule will decay not occur. For example, a proton cannot decay into three electrons because charge conservation would be violated, even though it is energetically possible.

QUESTION:
I think that it is possible to travel faster than speed of light. I explain it in this link. Is it correct?

ANSWER:
No, it is not correct. In your example, an earth-bound observer observes the traveler to travel 4.24 ly in 4.28 years. The traveler, as you correctly surmise, observes the trip to take 0.604 years. However, you have not taken length contraction into account. The traveler observes the distance she has to travel to be 4.24/γ =0.598 ly, so she perceives her speed to be 0.99c.

QUESTION:
So if black holes suck in everything in including light that must mean everything is getting pulled in as fast or greater then the speed of light. So if light is weightless and it is sucked in. What happens to any mass as it is sucked in. Would the mass of the object then cease to have mass? Because im pretty sure anything traveling at the speed of light has to be mass-less correct? And how does gravity effect something with no mass? I dunno if it is a good question or not but i couldnt find a whole lot on the subject.

ANSWER:
Nothing ever goes faster than the speed of light and only light can go at the speed of light. When an object merges with the black hole, its energy, E=mc ², is not lost and the black hole becomes more massive by the amount of the mass energy. When light is swallowed by the black hole, the mass increases even though the light does not have any mass because light does have energy and the energy shows up as increased mass of the black hole, m=E/c ².

QUESTION:
What happens gravitationally when the center of mass can no longer be considered a point but is instead an area? Specifically, suppose the Sun was to "explode" or supernova; ignoring the obvious destruction of the solar system, what would happen to the planetary orbit of Earth? I presume it would be roughly akin to letting go of the string at the end of which I have a ball spinning around me.

ANSWER:
The center of mass is always a point. If the sun were to "explode", the center of center of mass would continue to be at the center of where it was before the explosion. A star explodes approximately isotropically, that is, material goes out at the same rate in all directions. So, until the material reached the earth's orbit, the orbit would be unchanged. But, as material gets outside the earth's orbit, only the material inside would contribute to the force felt by the earth (this is Gauss's law). So the earth would behave as if there were a star of constantly decreasing mass at the original center of mass.

QUESTION:
okay, so i wanted to ask what would be the KE of a tungsten rod of length 70 m with a conical end of height 10 m, 6 m in diameter at one end and 6 cm at the other , weighing 38307.5 tons and falling at terminal velocity which i think is about 2340530 m/s?

ANSWER:
The speed, while large, is still less than 1% the speed of light, so you can use the classical expression for kinetic energy, KE=½mv ²=½x3.83x10⁷x2.34x10⁶=4.48x10¹³ J. Note that the composition, size, and shape are irrelevant. Since everything else was in SI units, I assumed that ton is metric tonne, 1 tonne=1000 kg. This must be some kind of projectile in a computer game.

QUESTION:
Can an electric current flowing in a wire be stopped by a magnetic field? If so, how? I need to stop it from distant.

ANSWER:
The magnetic force on a moving charge is always perpendicular to its velocity. To stop a moving object you must apply a force antiparallel to its velocity.

QUESTION:
I bought a 400lb gun cabinet and need to pull it on a 2 wheel hand cart up a 12ft ramp at about 35degrees to the horizontal How much load does 1 or 2 people have to carry and how much is borne by the wheel. I am trying to make sure we can be comfortably safe!

ANSWER:
I could make a rough estimate but would need to know the dimensions of the cabinet, if the center of gravity is near the geometrical center. I would assume that the cabinet was parallel to the ramp when being pulled.

FOLLOWUP QUESTION:
It is 20X29X55. It would not be parallel to the ramp but about 20 degrees from the ramp (which is about 35 degrees to the ground (thus avoiding 4 steps).

ANSWER:
Since only an approximation can be reasonably done here, I will essentially model the case as a uniform thin stick of length L with weight W , normal force N of the incline on the wheel, and a force F which you exert on the upper end. In the diagram above, I have resolved F into its components parallel (x) and perpendicular (y) to the ramp. Next write the three equations of equilibrium, x and y forces and the torques; this will give you the force you need to apply to move it up the ramp with constant speed.

Σ F _x=0=F _x -W sin θ
Σ F _y=0=F _y +N-W cos θ
Σ τ=0=½WL cos( θ+φ )-NL cos φ.

I summed torques about the end where you are pulling. Putting in W=400 lb, θ=35º, and φ=20º, I find F _x=229 lb, F _y=206 lb, and N=122 lb. Note that you do not need to know the length L. The net force you have to exert is F=√[(F _x)²+(F _x)²]=308 lb. If someone were at the wheel pushing up the ramp with a force B , that would reduce both F _x and F _y. This would change the equations to

ΣF _x=0=F _x-W sin θ+B
ΣF _y=0=F _y+N-W cos θ
Στ=0=½WL cos( θ+φ )-NL cos φ+BL sin φ.

For example, if B=100 lb, the solutions would be F _x=129 lb, F _y=169 lb, and N=159 lb; so your force would be F=213 lb.

QUESTION:
Imagine if you wrapped a rope tightly around the earth. How much longer would you have to make the rope if you wanted it to be exactly one foot above the surface all the way around?

ANSWER:
I hope you don't think that the rope would spontaneously rise up if it were longer than the circumference of the earth; you would have a slightly slack rope laying on the ground. You are specifying the difference in radii between one circle with a circumference C and another of circumference C+ δ; that is not really physics. But, it is easy enough to do. If C is the circumference of the earth, then C=2πR where R is the radius of the earth and C+ δ=2πR' where R' is the radius of the circle your rope would make if δ=1 ft. Then δ=2π(R'-R)=2π=6.28 ft. Note that δ depends only on how high the rope is above ground, not how big the earth is: if the earth were 1 ft in radius and you increased the length of the rope by 6.28 ft, the rope would be 1 ft above the surface!

QUESTION:
I'm writing a research paper for my college english class and the topic is Thorium Reactors. My question is "Are thorium based reactors such as LFTR fusion or fission and based?" I was just wondering because the it seems from what I've learnt that the reactors use the thorium to produce a reaction that makes another element such as uranium 233 which I assume is fusion because I'm sure they're using the energy put off from that initial reaction to power something. But after the uranium 233 is used and to produce energy as efficiently as possible I would think that you would implement a system that would immediately and directly use said produced uranium into some form a fission reactor.

ANSWER:
Fusion always involves light nuclei and there is no such thing as a fusion reactor, only ideas for them. So a thorium reactor must be a fission reactor. It would be inaccurate, though, to call thorium the fuel because thorium is not fissile. If a thermal neutron is absorbed by a fissile nucleus, it will fission and result in more neutrons leading to more fissions and the reaction can be self-sustaining. Thorium, which is 100% ²³²Th, absorbs a neutron to become ²³³Th which β-decays to ²³³Pa (half life 22 minutes)which β-decays to ²³³U (half life 27 days). The ²³³U is fissile and is nearly stable (α-decay half life 160,000 years). Thorium is said to be fertile, absorption of a neutron results in production of a fissile fuel. So a thorium reactor is a breeder reactor, a reactor whose purpose is create fuel. At the startup one needs a starter fissile fuel as well as the thorium to provide neutrons to create the ²³³U. As the ²³³U builds up, it becomes the fuel.

QUESTION:
Would it be physically possible to create a parachute capable of delivering a main battle tank safely to a theatre of war? Like how huge would it have to be?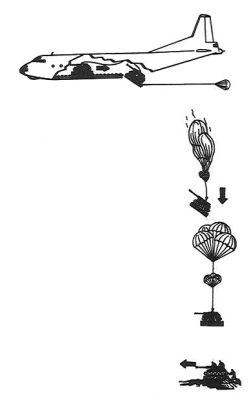

ANSWER:
A reasonable estimate of the force F of air drag on an object of mass m, speed v, and cross sectional area A is F=¼Av ²; this works only in SI units. The speed v when F=mg is called the terminal velocity. I estimated a reasonable terminal velocity would be the speed the tank would have if you dropped it from about 10 m, v≈14 m/s. The mass of the MBT-70 (KPz-70) is about 4.5x10⁴ kg. Putting it all together, I find that A≈10⁴ m², a square about 100 m on a side or a circle of radius about 30 m. You could do a more accurate calculation but this gives you a reasonable estimate.

QUESTION:
If you stand holding a box but the box is not moving, are you doing any work?

ANSWER:
See an earlier answer.

QUESTION:
Why is it necessary to have a minimal temperature of 150 million degrees Kelvin for nuclear fusion on earth if the sun does nuclear fusion at a temperature of 15 milloin degrees?

ANSWER:
There is more than one reason that I can think of. The mass of the sun is 2x10³⁰kg, quite a bit bigger than the mass of fuel in a fusion reactor. Therefore the rate of fusion in the sun can be low but the energy output would still be huge. Increasing the temperature would increase the rate. The density of the sun's core is about 150 g/cm³, 150 times more dense than water. In a fusion reactor, the practical densities are many orders of magnitude below this. Again, the rate of fusion would be dependent on the density of the fuel.

QUESTION:
My name is Justin and my friend Richard blew my mind when he told me that nothing doesn't have mass. Again. Nothing doesn't have mass. Is this true? I was taught that everything has an inherent mass. Is he wrong? Am I wrong? Does sheer nothingness have a mass or not. Please help me. My friend just blew my mind and I'd like it to be back together.

ANSWER:
It is true that the vacuum does not consist of nothing. See a recent answer for more detail. However, the vacuum does not contain mass in the sense you normally think of it—you cannot "weigh" a vacuum. Also, photons, the quanta of light, do not have mass. Until recently it was thought that neutrinos have no mass; they actually do have very tiny masses. All the double negatives in your question and my answer make this a little confusing; I hope I have answered what you meant to ask!

QUESTION:
in classical physics angular momentum is a variable factor, but why in quantum mechanics angular momenta are quantized. and how its related to spin. I have read that Paul Dirac showed, how changing some relativistic factors in Shroedinger's equation can spontaneously lead to the "spin" concept. but what the spin actually tells us and how we can visualize it.

ANSWER:
The reason why orbital angular momentum is quantized is that, when you solve the Schrödinger equation for the atomic wave function, the wave function is not normalizable unless the angular momentum is ħ √[L(L+1)] where L is an integer. (For our purposes here, "not normalizable" means that the wave function becomes infinite somewhere.) It also turns out that L is called the orbital angular momentum quantum number and its being an integer has nothing to do with spin except that spin is also an angular momentum. To visualize spin, read two earlier answer (#1 and #2). In relativistic quantum mechanics, the Dirac equation replaces the Schrödinger equation. When you write the Dirac equation for an electron, it turns out that spin is indeed predicted to have an angular momentum quantum number of ½ as is observed experimentally.

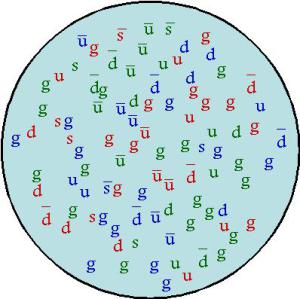
QUESTION:
I've just found out that a proton isn't made up of two up and one down quark but also contains zillions of other up and down quarks along with their anti matter equivalents. Here's a link to an article from the L.H.C people at Cern that shows this. I'm amazed and confused because I thought that matter and anti matter particles would annihilate each other. Why don't they? And, if they do, how is the 'zillions of other quarks' balance maintained?

ANSWER:
The crux of what is going on here is that a vacuum is not really a vacuum as we generally think of it—nothing. Particle-antiparticle pairs are continuously popping into existence and then annihilating back to nothing after a short time. This is called virtual pair production. Also, if a particular particle experiences a particular force, the messenger of that force (gluons for the strong interaction, photons for the electromagnetic interaction) are continuously being emitted and reabsorbed. All this is called vacuum polarization. So, I could give you a similar description of the hydrogen atom: the hydrogen atom is not really a proton and an electron, it is a proton and zillions of electrons and positrons and photons. If you really want to understand the hydrogen atom in detail, you need to take the effects of vacuum polarization into account (see the Lamb shift, for example). The CERN explanation should have included zillions of positrons and electrons and photons inside the nucleus also. Just as a hydrogen atom is pretty well described as a proton and an electron as a first approximation, a proton is pretty well described as three quarks as a first approximation.

QUESTION:
Why the whole matter of radioactive sample does not disintigrate at once or Why it always take half life to disintegrate half of initial value?

ANSWER:
Because decay is a statistical process. Whenever you have a large number N of anything they will, at some time t, have a time rate of change R=dN/dt. If R<0, N is getting smaller (as in radioactivity) and if R>0, N is getting larger (like bacteria growth). For a great many cases in nature, it turns out that the rate is proportional to the number, R ∝N. Radioactivity turns out to behave that way: if you measure R for 2x10²⁰ radioactive nuclei it will be twice as big than when you measure R for 10²⁰ nuclei. You can then solve for what R is for a given situation: dN/dt=-λN where λ is the proportionality constant, called the decay constant; the minus sign is put there so that λ will be a positive number since the rate is negative. If you know differential equations, you will find that N=N ₀e ^-λt where N ₀ is the number when t=0. The decay constant is related to the half life τ _½=ln(2)/λ. However, this all depends on there being a large number to start. In the extreme case, if N ₀=1, they would all decay at once! You just could not predict when. If N ₀=2, they might both go at once or else one might go before the other but not necessarily at τ _½.

QUESTION:
When solving questions involving two identical springs being stretched to points A and B to create a total length and the natural length of the springs are given. What is a consistent way to calculate the amplitude? Is it half of the length of AB subtract the natural length of the spring?

ANSWER:
I assume that the springs are in series—one attached to the end of the other. Suppose that you exert some force F such that the springs are stretched by a distance s. Then each spring will be stretched by ½s. If k is the common spring constant, F=½ks. Therefore the two together behave like a single spring with spring constant ½k.

QUESTION:
How fast are we moving? Besides Earth rotation and revolving, there's our path in the galaxy, and even greater in relationship to all other galaxies, and please include the expansion of space-time.

ANSWER:
First you should understand that it only makes sense to ask what our velocity is relative to some inertial frame of reference. And, also, it depends on things like what time of day it is, what time of year it is, what year it is, etc. because all these things affect your velocity; e.g., relative to the earth's axis, you are moving in opposite directions at noon and midnight. There is a nice qualitative discussion of this question at Curious about Astronomy; adding up all the various velocities, she finds a maximum speed relative to the center of our supercluster of about 900 km/s. Given the roughness of this calculation, trying to fine-tune it by adding in the expansion of space-time is pointless.

QUESTION:
In my AP Physics class, we have had a class-wide debate over a physics problem for the last few days. The problem asked how much work it would take to move a satellite that was orbiting Earth at a certain height to a greater height. Some of us say that the work equals the change in potential energy, while others say that the work is the change in the total mechanical energy. The total energy method gives an answer of exactly half of the amount the potential energy method gives. Who is right? Both orbits are circular.

ANSWER:
Since the speeds in the two orbits are different, the kinetic energies will be different, so the correct way to do this is
½mv ₂ ²-mMG/r ₂ ²=W+½mv ₁ ²-mMG/r ₁ ². Of course you will have to figure out what the velocities are in terms of the radii, but that should be a piece of cake for AP students!

QUESTION:
A car is travelling 45 mph, with the road being at a 5-8% incline. How long would it take a car to slow down without using breaks? This is not homework. I am a claims examiner that is trying to get some information as to the rate of speed in which a car decelerates.

ANSWER:
You are a claims examiner and you spell brakes "breaks"?! I could do this if I assumed no friction whatever, but it would not be predictive of the real world because there is plenty of friction acting on a moving car even without brakes applied. I could make a better estimate if you could tell me how far this particular car, starting at 45 mph, traveled on level ground with brakes not applied. Also, is the car in gear? In neutral? Engine running? If there were absolutely no friction, the car would keep going until it had gone vertically up a distance of about 20 m≈66 ft regardless of the grade of the incline. For a 6% incline, the distance traveled by the car would be about 1100 ft. In the real world it would be way less than this.

QUESTION:
As we know the earth is revolving around the sun. Why don't we have any feeling of revolving?

ANSWER:
In order to have a "feeling" of motion, there must be an acceleration. The acceleration of the earth in its orbit is about 6x10^-6 m/s². For comparison, if you are in a car with an acceleration from 0 to 60 mph in 10 s, your acceleration is about 3 m/s²; this means that you "feel" pushed back into your seat with a force about one third of your weight. The force you "feel" due to the orbital motion of the earth is about 1/600,000 of your weight, far less than you could "feel". The acceleration due to the earth's rotation on its axis is larger than this but still way smaller than you could "feel".

QUESTION:
Trying to understand a relationship between nuclear physics and particle physics. In nuclear fusion 4x H1 fuses to give (ultimately) 1 x He4 + 1 positron a neutrino and energy. However, 4 protons have become 2 protons and 2 neutrons and neutrons are more massive than protons - so we have apparently gained mass - which should require an input of energy. My research finds that the He4 nucleus is less massive than the 4 protons that made it because mass has been converted to 'binding energy'.

Questions:

Since a lot of the mass of a proton comes from energy, doesn't this 'binding energy' add mass to the He4 nucleus?
The protons that formed this nucleus are made up of Quarks held together by energy in the form of the exchange of Gluon particles. To convert to a neutron, an Up Quark has become a Down Quark with more mass. What mass has the He4 Nucleus lost?
Do the Quarks in the He4 nucleus have less mass than those in the H1 since the Quarks appear to be the only mass in the process that can convert to energy? Surely if the energy came from the Gluons it would still just be energy and hence not have the mass/energy conversion ratio?
If the energy did come from the Gluons, are Quarks in He4 less tightly bound than those in H1?
Does this continue to occur as you move up the fusion sequence to higher mass elements?
Has the creation of matter from energy (e.g. the electron produced in this fusion) ever been actually achieved? Or are we working purely on theory based on remote observation of the Sun?

ANSWER:
I should really delete this question altogether because it has ignored the site ground rules stipulating " …single, concise, well-focused questions…" However, I will address at least parts of the question to clear up some major misconceptions. Although the questioner asserts that he is " trying to understand a relationship between nuclear physics and particle physics", I will ignore all questions relating to quarks and gluons because if the nuclear physics itself is not understood, then there is no point in trying to relate it to particle physics. To understand the fundamentals of nuclear physics, you do not need to even know that quarks and gluons exist, only that a strong nuclear interaction exists. In the opening paragraph the mass of the ⁴He nucleus is compared to the mass of four protons. This is a meaningless comparison because the constituents are two neutrons and two protons. (See below* for how protons are converted into ⁴He nuclei.) Indeed, the mass of the ⁴He nucleus is less than the mass of its constituents. If one knows E=mc ², the reason for this mass difference is intuitive. Does it take work to pull a proton or neutron out of the ⁴He nucleus? Of course it does, otherwise the ⁴He nucleus would not stay together. So energy must be added to disassemble the nucleus and this energy resides in the greater mass of the constituents. I find this much easier to understand than to say that the excess mass of the constituents is "converted" to binding energy.

As you move up to create heavier and heavier nuclei via fusion, the fusions continue to release energy but in decreasing quantities until the final product is iron. Thereafter, if you want to fuse nuclei, you must add energy. So, elements heavier than iron are not produced in stars. Heavier elements are produced in supernova explosions.

You ask if "…creation of matter from energy…" has ever been observed. It happens all the time. But that is really the wrong question because matter and energy are not different things, matter is simply a form of energy. So, for example, if you fused two ³²S nuclei to a single ⁶⁴Ge nucleus, the Ge would have more mass than the two S. Any time you have an endothermic chemical reaction you end up with more mass than you started with (although almost immesurably small because chemistry is so inefficient).

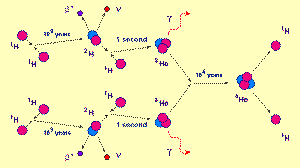
*As can be seen in the figure above, the proton-proton cycle requires an input of 6 protons and ends with one ⁴He and 2 protons. So the net input is 4 protons. However, there are numerous outputs—2 positrons, 2 neutrinos, and 2 photons, all of which carry energy away. That is why comparing the net input with the final product is not meaningful.

QUESTION:
The substance which undergoes deformation with a small force will be elastic or inelastic?

ANSWER:
You cannot judge the elasticity of something by how easily it deforms. If it stays deformed after the force is removed, it is inelastic. If it returns to its original shape after the force is removed, it is elastic.

QUESTION:
The particles that make up a rock are constantly moving. However a rock does not visibly vibrate. Why do you think this is?

ANSWER:
The amplitude of the vibration is less than the distance between atoms in the rock, ~10^-11m. The atoms are all randomly vibrating so that there always as many atoms moving in one direction as in the opposite direction. The frequencies of the vibrations are ~10¹³Hz, far above a frequency which you could feel, hear, or see.

QUESTION:
I was just wondering if you have ever thought that dark energy was actually just gravity? Could the gravitational force act differently over large(r) scales? This seems like something I would like to study at a PhD level as this could be an area to reveal the connection between gravity and quantum mechanics.

ANSWER:
The best theory of gravity is general relativity (GR). GR already contains a term, called the cosmological constant, which can add a repulsive force to the attractive gravitational force. I do not quite see how this could be a route to quantizing gravity, but who knows? Good luck!

QUESTION:
A quantity of electrical energy is defined by volts x amps x time. A quantity of mechanical energy could be defined (or is) by force x distance which equates to kinetic energy. When electrical energy is converted into mechanical, a force can be created by applying voltage and current (amps). Is this a paradox? Electrical energy is functionally force x time while mechanical energy is force x distance.

ANSWER:
1 V=1 J/C and 1 A=1 C/s, so 1 volt·amp·second=1 Joules=force·distance. No discrepancy, no paradox. Another way to look at this is that current times voltage is power and power is W=J/s.

FOLLOWUP QUESTION:
I totally understand that 1 amp is 1 coulomb per second. I don't know where 1 volt is equal to 1 joule per coulomb comes from or why that is true.

ANSWER:
The electric field E is defined to be the force F felt by a charge Q divided by Q. The electric potential V is defined as E times distance d over which it acts. V=Ed=Fd/Q=[J/C]

QUESTION:
If gravitons mediate the gravitational force between particles, how does this work for a black holes where gravitons cannot escape the event horizon? Are gravitons predicted by General Relativity?

ANSWER:
See an earlier answer. Gravitons are not predicted by general relativity. Physics inside the event horizon is not well understood.

QUESTION:
Why is there a slightly rough surface on a basketball? Does this affect the static friction acting between your hand and the ball during a shot?

ANSWER:
The dimples on a golf ball and the fuzz on a tennis ball reduce air drag and thereby allow the ball to go faster and farther. However, the speeds of these balls are much larger than speeds ever encountered by basketballs and this cannot be the reason for the bumps on a basketball. A little research reveals the purpose is just to make the ball easier to grip and handle, as you speculated.

QUESTION:
Are there any known stable nuclei for witch Z>N? Why are they so rare?

ANSWER:
The only stable Z>N nucleus is ³He. The reason that all stable isotopes heavier than helium have the same or more neutrons than protons is complicated because the nuclear force is complicated. One important reason is that the repulsive Coulomb force as well as the attractive nuclear force is present trying to blow the protons apart and the more protons you add, the more important this becomes; adding neutrons tends to push the protons farther apart to reduce the repulsive force. Neutrons are sort of "insulation" for the protons' electric repulsion from each other.

QUESTION:
Electrons orbit around the nucleus in varying degrees of proximity to the nucleus. Do electrons farther from the nucleus orbit at a different rate of speed than those closer to the nucleus?

ANSWER:
Yes, if you use a Bohr model for the electrons. However, the notion of electrons running around in well-defined orbits is naïve and incorrect.

FOLLOWUP QUESTION:
Would it be correct to apply Kepler's Laws of Motion to the revolution of electrons about the nucleus in the Electron Cloud Model?

ANSWER:
The electrostatic force is a 1/r ² force just like the gravitational force, so if the atom were a classical system Kepler's laws could be used for an atom. In fact, the Bohr-Sommerfeld model, the first extension of the Bohr's circular orbit model, essentially does this by including elliptical orbits and appropriate quantization. Of course, the atom is not a classical system and although such models can be instructive, they are not strictly accurate. What you refer to as the "electron cloud model" would be the proper solutions to the Schrodinger equation, not having well-defined orbits.

QUESTION:
I would like to know if one horsepower is equivalent to 33,000 pounds per minute, and for a four cycle engine fires on every 2nd revolution of the crankshaft, and lets just say this 1 hp engine runs at 2800 rpm , so it fires 700 times , is there a formula to calculate how much force was created in the combustion chamber in pounds?

ANSWER:
Power is energy per unit time; some possible units of power are Watts (W), horsepower (hp), and foot-pounds/second (ft-lb/s). So your lb/min is not an acceptable unit for power because lb is a unit for force, not energy. But, you apparently looked this up somewhere because 1 hp=33,000 ft-lb/s. The power of the engine does not tell you the force in the combustion chamber, in fact force is not really what would be of interest. What you want is the energy delivered by each piston for each stroke. If the pistons fire, for example, at the rate of 1000 times per minutes, each piston delivers 3300 ft-lb per stroke.

QUESTION:
I knew that when a car which travels very fast and is brake very sudden, the car will like "fly away". But is there any theory or principle or rule can explain this?

ANSWER:
I do not know what "fly away" means.

FOLLOWUP QUESTION:
To explain, an illustration is made. Imagine a bicycle that travels in very high velocity and it is braked suddenly and hardly, what will happen. The bicycle will like "flying up" caused by the momentum. It is also related to the principle of acceleration and deceleration.

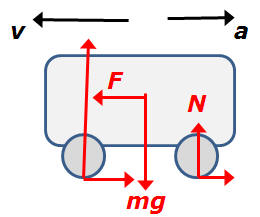
ANSWER:
OK, I get it now. Refer to the figure above. The easiest way to do this is to introduce a fictitious force. If the car is accelerating with acceleration a (which points opposite the velocity v when braking), Newton's first law will be valid in the car frame if a force F=-ma acting at the center of mass (COM) is introduced. The "real" forces on the car are a normal forces up on each wheel by the road, the frictional forces backwards on each wheel by the road, and the weight mg which acts at the COM. In the drawing I have only labeled the weight, the normal force on the rear wheel, and the fictitious force because those are all you need to answer your question. If you wish, you could find both normal forces and the sum of the two frictional forces in terms of a; if all wheels were locked you could find the individual frictional forces if you knew the coefficients of kinetic friction. Now, I will sum torques τ about the point where the front wheel touches the ground, Στ=mah+NL-mgs=0 where h is the height of the center of mass above the ground, L is the horizontal distace from the front axle to the COM, and s is the horizontal distance between the wheels. You can now solve for N, N=(mgs-mah)/L. Now think about N; if N<0, the road would have to pull down on the back wheels to hold the car from rotating forward about the front wheels. N will be zero when the car is just about to "fly up"; therefore, if a>g(s/h), the car will "fly up".

QUESTION:
If you aimed a high powered laser beam in a tangential direction to the surface of the Earth, would that beam travel in a straight line and shoot out into space, or would Earth's gravity be enough to at least bend the light in a measurable amount?

ANSWER:
See an earlier answer. If you calculate the angle for earth instead of the sun, φ=4GM/(c ² r)=0.002 arcseconds, just about impossible to observe.

QUESTION:
When speaking of particle accelerators,the accelerators keep adding energy to the particles, even though they cannot speed up any further. But where does the energy go?

ANSWER:
Well, they never really get to a speed where they cannot go any faster because they never reach the speed of light. I have always thought "accelerator" was a misnomer for very high-energy machines because the acceleration (rate of change in speed) is almost zero; I would prefer "energizer". The easiest way to think about it is that the particles acquire mass and that is "…where…the energy go[es]". The energy of the particles is E=mc ²=m ₀ c ²/√[1-(v/c)²] where m ₀ is the mass at rest. For example, if v/c increases from 0.99 to 0.999, that is only a 1% change in speed; but the energy increases from 7.1 m ₀ c ² to 22.4m ₀ c ², more than triple.

QUESTION:
A cylinder is kept in friction less inclined plane (curve face touching incline). Why it does not roll (transnational motion only) although a torque is working on it with respect to contact point due to component of force parallel to incline

ANSWER:
Because the cylinder is accelerating. The point of contact is also accelerating and so you cannot use it as a point about which to sum torques because Newton's laws are not valid in an accelerating coordinate system. An accelerating coordinate system is called a noninertial frame. There is, however, one point where you can always sum torques even if that point is accelerating—the center of mass. The net torque about the center of mass is zero because the weight vector acts at that point and the normal force passes through it.

QUESTION:
I am looking for relationship between viscosity of air and pressure. I want a table listing the viscosity at different pressures. Pressure should start from 0.1 atm to 1 atm.

ANSWER:
The table above comes from an article by Kadoya, Matsunama, and Nagashima. Pressure is given in MPa and 0.10 MPa=0.987 atm≈1 atm. So you want the variation between 0.01 MPa and 0.1 MPa. As you can see the variation is very small; the viscosity is much more dependent on the temperature.

QUESTION:
Two questions for you concerning the recent proof that gravity flows in waves. 1). How fast do these gravity waves move? Do they move at a constant speed or is their speed predicated by the mass of the object that generated the waves? 2). Since the earth is trapped in orbit around the sun by the sun's gravity, how can a wave moving out from an object in turn pull a second object back towards the object that generated the wave? In other words, how can gravity waves moving out from the sun at the same time pull the earth towards the sun?

ANSWER:
The answer to your first question is in a recent answer. In your second answer, you are confusing gravity with gravitational waves. Our picture of gravity is that mass (like the sun) deforms the space around as in the animation above. Something like the earth orbiting the sun is not really feeling a force, it is following the contour of the space. (Do not take this simplistic model too seriously, it is really the four-dimensional space-time which is "deformed".) But, if something accelerates, like the earth going around in its orbit, it will send out ripples and those are the gravitational waves. On the scale of this animation, the waves the orbiting earth is sending out are far too tiny to be seen. But, if the objects orbiting are much more massive, like the two orbiting black holes which were observed in the recently reported observation of the waves, the waves are much bigger.

QUESTION:
Ok so you know how they say, "if you look up at the stars in the night sky, you are seeing light that's taken millions of years to travel to earth, so you are seeing Into the past potentially"? Ok so here's the question. If say I'm on a planet in the Andromeda galaxy, and you're on earth looking at me with a super telescope( to where u can actually see me wave at you) and let's say we agreed on a specific time and date to do this. If I start waving at you at the exact time you are observing me with the telescope, do you ever see me wave or does it take millions of years to see me wave at you ?

ANSWER:
How do you plan to agree on a specific time and date to wave if it takes millions of years to communicate. Just imagine that there is a star exactly halfway between you and me and we have, by some magic, both been instructed to do our things (wave and look) when we observed the star to become a supernova. If you and I are separated by a million light years, I will not see you wave until a million light years have passed. Furthermore, the supernova would have occurred a half million years before either of us saw it.

QUESTION:
Why is it that when I listen to music on my PC through an external speaker set and my cell phone right next to me gets messages, etc... and they cause distortions in how the music sounds?

ANSWER:
Your cell phone is both a receiver and a transmitter of radio waves. The transmitted radio waves may be detected by your sound system.

QUESTION:
I mean to say the angle derived in Einstein equation φ=4GM/(c ² r)=1.75 arcseconds is total deflection when light source is opposite side of the Sun?

ANSWER:

QUESTION:
When a television set is turned on it often generates an electrostatic field. You can still feel this charge if you move your arm near the screen shortly after the set has been turned off. Why does this field not disappear as soon as the television set has been turned off?

ANSWER:
You probably have an old cathode ray tv. The screen is coated with a phosphor which glows if you strike it with an electron. Electrons are shot from the rear of the tube to cause a picture to be formed. Some of these electrons are still on the screen when you turn off the power.

QUESTION:
Ships are often built on ways that slope down to a nearby body of water. often a ship is launched before most of its interior and superstructure have been installed and is completed when a float. Is this done because the added weight would cause the ship to slide down the ways prematurely?

ANSWER:
Friction can be a tricky business, but the simplest behavior is that the frictional force increases proportional to the weight. But the force of the gravity trying to slide the weight down the slope is also proportional to the weight. Therefore, doubling the weight of the ship should not increase its tendency to slide down. Besides, if this were a concern you could always temporarily block the path down the slope like placing blocks in front of a vehicle on a slope to keep it from rolling. I suspect the real reason is that the structure of the ramp is probably not strong enough to support the full weight of the ship.

QUESTION:
If one wanted to turn a cylinder 5 feet in outer diameter and 3 feet inner diameter and the reel is supported via a 2 in bar through the center of it Look like this i suppose (more like a reel) A rope is wound around the outer diameter and pulled (think of a yo yo) how much torque would you have to put on the rope to get it to turn? at 35 rpm? Can you show how one can figure that?

ANSWER:
It would depend on how long you pulled, what the mass of the hollow cylinder is, and how much friction there is.

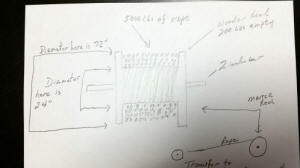
FOLLOWUP QUESTION:
I have asked several people to give an answer on this and no one has been able to answer it for me. So I attached a pic I just drew out for you... On the pic you see that the master reel is 5000 lbs... I want to pull the rope off the reel and put on another reel... I would like to do so at 35 rpm on the small reel... The small reel is just like the large reel but the OD is 24 inches and the center of the reel is 12 inches... with a bar going through it just like the large one... how much pulling torque would be needed to get the large reel to start turning... neglect friction...not enough there to consider...

ANSWER:
First you have a misconception. If friction is truly negligible, any torque, no matter how small, will start the big reel turning. It is a matter how long you want to wait until you get up to 35 rpm on the smaller reel. For several reasons this is a quite complicated engineering problem. The most important problem to deal with, I think, is that as rope comes off the larger reel its weight gets smaller and its radius gets smaller; at the same time the smaller reel gets larger and heavier. So if you want to keep the smaller reel going at a constant 35 rpm the larger reel will have to change its speed if the rope is to remain taught. So, I will only address the question of how you start up just to demonstrate how torque determines what happens. From your drawing, it looks like the rope fills the reel so its outer radius would be about 3 ft≈1 m and its inner radius would be about 1 ft≈0.3 m. Since the mass of the rope is 5000 lb≈2300 kg is large compared to the 200 lb reel, I will neglect the contribution of the reel; this simply says that the torque you apply mainly has the effect of getting the rope spinning. Since it is the smaller reel you want to go 35 rpm, the upper reel would need to have an angular velocity of (0.5/3)x35=5.8 rpm=0.61 radians/s. (Assuming that your idea is to use the empty reel to pull the heavier reel via the rope.) Again, I will neglect the torque necessary to get the smaller reel going since it will presumably be lighter than the already neglected weight of the heavier reel. The basic physics principle to use is the rotational form of Newton's second law, τ =Iα where α is the angular acceleration, τ is the torque, and I is the moment of inertia. In your case, the angular acceleration would be the final angular speed divided by the time to get there; so if you want to get up to speed in 10 seconds, the angular acceleration would be 5.8/10=0.58 rpm/s=0.061 radians/s². You see, now, why there is no answer to your question: the torque will depend on how quickly you want to get up to speed. The moment of inertial of the rope is I=½M(a ²+b ²)=½(2300)(1²+0.3²)=1250 kg·m². Finally you can estimate the torque τ =1250x0.061=76 N·m=56 ft·lb. A longer spin-up time would need a smaller torque.

QUESTION:
I've got a basic question about signal processing within the discipline of management information systems. Today, some basic signals within management information systems, which people come across are electrical, light (fiber optics), and radio waves. Is it true that radio waves are a type of electromagnetic radiation or many types of electromagnetic waves, which can travel at the speed of light? Is that true? I didn't think it was possible for anything to travel at the speed of light. As I understand it, the speed of light in a vacuum, such as space or other, commonly denoted c, is a universal physical constant that's very important in many areas of physics. The speed of light, it travels (approximately 3.00×10⁸ m/s) or 186,000 Miles per second. Can anything you know of travel at the speed of light especially radio waves?

ANSWER:
When a physicist refers to "the speed of light" she is talking about the speed of electromagnetic radiation in a vacuum. Of all the possible wavelengths of light, visible light is but a tiny fraction.

QUESTION:
Whether light is a particle or wave? Which is right and why?

ANSWER:
Light is not a particle or a wave, it is a particle and a wave. This is called wave-particle duality. If you design an experiment to observe a particle, you will observe a particle; and, if you design an experiment to observe a wave, you will observe a wave.

QUESTION:
If you have a wind up toy car, meaning that when it starts you can wind it up to maximum and have a constant force pushing it forwards, how would you expect the distance in travels to change as you add mass to it?

ANSWER:
The spring will deliver a certain amount of energy. Giving the same amount of energy to a large mass and a small mass will result in the small mass going faster. The small mass will therefore go farther. This assumes that the wheels never slip.

QUESTION:
If all things with mass have a proportional amount of gravity and gravitational waves were recently observed to have been produced by 2 black holes converging, is it correct to deduce that all things with mass produce gravitational waves proportional to their mass?

ANSWER:
Yes. Any object with mass which accelerates should radiate gravitational waves. Wave to someone and you cause gravitational waves. However, gravity is the weakest force in nature so, for the the waves to have a big enough amplitude to be detectable, the masses must be extremely large (as in black holes).

QUESTION:
How fast do gravitational waves move? Is that rate constant?

ANSWER:
The speed of gravitational waves has never been measured. The speed at which a gravitational field propogates should be the same but it has never been measured either; this would determine, for example, if the sun suddenly disappeared how long it would be until the earth stopped orbiting. The theory of general relativity, which predicts gravitational waves, say that the speed of gravity should be the same as the speed of light. The recent observation of gravitational waves determined the distance to the source to be about 1.33 billion light years, but the uncertainty was very large, about 40%, so it really provides no measurement of the speed. Whatever the speed, there is no reason to think that it would not be constant everywhere in empty space.

QUESTION:
A car is moving forward through a road. Which part of the wheel of the car moves fast- the upper part or the lower part of the wheel?

ANSWER:
Inasmuch as the part of the tire in contact with the road is at rest, the answer should be obvious. You should be able to show that the top of the wheel is moving forward with twice the speed of the car.

QUESTION:
Has anybody ever done the double slit experiment on a very large scale. By large I mean physically where the electrons are shot at tow slits several feet wide separated by an even greater distance from a large distance away to see if the electrons themselves will still manage to make it through the slits at all? As long as the electrons are unobserved acting as a wave they should still continue to go throught the slits and produce a wave pattern behind the slits regardless of scale. However does this deteriorate at some point and break down to cause the electron to again act as a particle and simply hit the mass between the two slits and if so could this be somehow used as a physical means to measure the energy of the electron? Could an electron with a greater energy then once again act as a wave?

ANSWER:
As far as I know, nobody has ever done a true double-slit experiment with electrons at all. Given the extraordinarily short wavelength of an electron, the spacing between slits would have to be on the order of 10^-10 m and you just cannot make physical slits that close because that is like the distance between atoms. What is actually done is to shoot electrons at a single crystal and you get a double-slit like experiment. For diffraction to be observable the slit spacing and slit width must be small compared to the wavelength of the wave.

QUESTION:
I am doing an experiment on factors affecting the travel distance of a toy car from down a ramp and thought it would be a good idea to understand how a physicist thinks of things. My question is, how do you think weight of an object affects the distance it will travel after going down a ramp?

ANSWER:
The best discussion I have seen of the physics of pinewood derby races is this youtube video. You will see that what matters more than the added weight is where you put it. (Thanks to my son Andy for pointing me to this video; his son and my grandson Finn placed second in the Cub Scout pinewood derby last year on the strength of the tips here!)

QUESTION:
Hello, question in physics. Why would the speed of a rollercoaster with potential energy of 5MJ have less than that predicted for a perfect frictioless track at the bottom of the slope?

ANSWER:
A roller coaster has wheels and some of the kinetic energy would be in their rotation, not in the speed of the cars. Of course, if the track were perfectly frictionless the wheels would not go around at all. Maybe your problem means no energy lost to friction? Or maybe the bottom of the slope is not at the zero of potential energy?

QUESTION:
What will happen if we fill water in the tyres of our cars instead of air?Does it have any effect?.

ANSWER:
Three important issues I can think of. First, it would add a lot of weight to the vehicle which would hurt your gas economy. Second, the moment of inertial of a wheel would be larger requiring a larger torque having to be exerted for either acceleration or braking. Third, air is compressible and water is not and so the wheel would not have a cushioning effect on the ride.

QUESTION:
We say that time slows as we accelerate. Is time some existent entity that can slow? Or is it the accelerated object [or particles it is composed of] that somehow "ages" more slowly because of the energy applied to it? i.e., is it the change in mass, and not time that slows aging?

ANSWER:
You do not need to talk about acceleration. Time dilation says that clocks which have a high velocity relative to you run more slowly than your clocks. And, it is not that they look like they are running slower, in fact they may look to be running faster, but they actually do run slower; see faq page for links discussing this. The best way to see this, I think, is to consider the light clock discussed in an earlier answer. To understand the light clock, you must accept that the speed of light is the same for all observers; see the faq page. Also, to help you with understanding time dilation, read about the twin paradox.

QUESTION:
What would happen if you threw a baseball at the speed of sound?

ANSWER:
At such a large speed, air drag has an enormous effect on ball. To see the mathematical details see earlier answers for a lacross ball and a baseball. I will make the same assumption that I did in those answers that the amount by which the ball will fall will be very small compared to its horizontal distance and the speed acquired in the vertical direction will be very small compared to its horizontal speed. So I will ignore the small effect which the vertical motion will have on the horizontal motion. As discussed in the earlier answer, the horizontal distance x and speed v are given by v=v ₀/(1+kt) and x=(v ₀/k)ln(1+kt) where v ₀ is the initial velocity and k is a constant determined by the mass, geometry, and initial velocity of the ball. For v ₀=340 m/s (speed of sound) and a baseball (mass=0.15 kg, diameter=0.075 m) these become v=340/(1+2.8t) and x=121ln(1+2.8t) and are plotted below.

In one second the ball goes about 160 m and slows down to less than 100 m/s. During the same time, the ball will fall approximately 5 m and so, if launched horizontally from a height of 5 m will hit the ground in one second as shown below. Be sure to note the difference in vertical scales; an insert shows the trajectory drawn to scale. The small distance fallen is the justification for my approximations above.

QUESTION:
Hi! I am new to Quantum Mechanics and I am a little confuse about the representation of the spin. So if I have a 1/2 spin particle I usually put spin up in the positive direction of Z axis and spin down in the negative one and the probability of getting spin up or down is proportional to the cos^2 of half of the angle between spin and the certain direction. But if I have multiple options for the spin (e.g. in spin one i have spin 1,0,-1) how do I visualize them? I mean If i put upward and downward in the z axis, and at z=0 for spin of 0 I don't get the probability one if I apply the above formula.

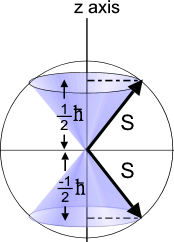
ANSWER:
I do not know what you mean about the "…cos² of half of the angle…", but you seem to not know what, e.g., spin ½ means. When you say spin s, this means that the spin angular momentum quantum number is s; this means that the magnitude of that spin angular momentum is S=ħ√[s(s+1)] where ħ is the rationalized Planck constant. But, there is another quantum number, m _s=-s, -s+1, -s+2, …, s-1, s which is the quantum number for the z-component of S, S _z=m _s ħ. Hence, the angle θ which the vector makes with the positive z-axis is θ=cos^-1(S _z/S). For s=½, θ=cos^-1(½/√(3/4))=54.7⁰ and θ=cos^-1(-½/√(3/4))=125.3⁰; similarly, for s=1, θ=45⁰, 90⁰, 135⁰ .

QUESTION:
Does a uniformly charged ring rotating at constant angular velocity about its axis perpendicular to its plane radiate electromagnetic waves? Because the magnetic field produced is constant hence there is no changing magnetic field and hence no em waves.is it ?

ANSWER:
Any accelerated charge radiates. The radiation from a charge moving in a circle is called synchrotron radiation. The theory of synchrotron radiation is very difficult and not appropriate to do here. I can tell you, though, that the energy which the charges have is so low that the power radiated would be immeasurably small.

QUESTION:
I just saw a music video in which a group of performers appear to be in an aeroplane cabin in free-fall for 2 minutes and 40 seconds. The choreography is spectacular, and it appears to have been done in ONE take! How far would the plane have had to descend to maintain zero gravity conditions for 160 seconds?

ANSWER:
This video was shot in Russia in a reduced-gravity jet provided by S7 Airlines. Weightlessness is not achieved by falling but by following the parabolic path which a projectile would follow. Imagine that someone shot you from a cannon with a speed of 500 mph (the typical speed of a commercial jet). If there were no air drag, you would follow a parabolic path. The plane which contains you now follows that exact path and that is how you appear to be weightless. An alternative way would be for the plane to simply go straight down with an acceleration of 9.8 m/s², but I think you can see that this would not be a very safe situation. Anyhow, back to your question, I could not find reference to any such parabolic flight lasting longer than 30 s, so the video must have been shot in more than one take. Because this is such an unfamiliar environment, I cannot believe that, even with a lot of practice, it could be done in a single take without errors. And, if the plane were simply falling for 160 s, it would have to have started at an altitude of about 80 mi (far higher than a plane can actually fly) and would end with a speed of about 3600 mph (far faster than the plane could fly without disintegrating).

QUESTION (submitted by my daughter!):
Is this exciting for you?? I dont really understand it but I'm trying to...it seems cool!

ANSWER:
Observing gravitational waves has been a holy grail of physics since before I was an undergraduate (like 55 years ago, gasp!). So yes, it is pretty exciting news. This is actually just the first direct evidence for gravitational waves. Indirect evidence was found when observing a pair of stars orbiting each other and spiraling in toward a collision. The loss of energy turned out to be exactly equal to the amount of energy they would lose if radiating gravitational waves. A nobel prize in physics was awarded in 1993 for this observation. The animation below shows the predicted gravitational waves from two neutron stars orbiting each other.

QUESTION:
A bit off beat from what you are usually asked. Jews are not allowed to drive a car on the Sabbath. The problem is the internal combustion engine which creates a spark in the piston igniting the gasoline. In a Tesla automobile does the magnetic field around the motor ultimately create a spark driving the wheels?

ANSWER:
It is natural, if you have a little knowledge about electric motors, to think of the magnetic field driving the motor. In fact, a magnetic field never does work because of its very nature. Although the presence of magnetic fields is imperative, work is always done by electric fields they produce. Most electric motors have "brushes", contacts which slide on the rotating armature, and small sparks are inevitable when electrical contact is made or broken. The Tesla electric car, however, employs a type of motor called an induction motor which is brushless and is therefore probably sparkless.

QUESTION:
Hi this may be a hard question but If I wanted to run 2200 gpm through a 2500 foot run with 50 feet of fall what size pvc pipe would this take? This is all gravity.

ANSWER:
At first I just did a calculation with no corrections for viscosity or drag. I found the velocity had to be about 17 m/s and the diameter of a pvc pipe would have to be about 0.1 m≈4 in. But then I worried about the fact that a pipe that long is likely to have significant drag over its length. It is a pretty complicated engineering calculation and I was unfamiliar with many of the parameters. But I did find a web site which seems to have made it easy for me by including a calculator. Frankly, I have no idea what the roughness coefficient is, but it suggests a value of 150 for plastic. The result is below. As you can see, to get a flow rate of about 2200 gpm would require a pipe with diameter of about 10 in.

QUESTION:
What if Einstein's General relativity wrong? Would all physics need to be rewritten?

ANSWER:
Actually, the theory of general relativity, essentially the theory of gravity, has very little effect on most of physics. Furthermore, like all theories, it is an idealization and approximation and is already "wrong" at some level. It is also incomplete because there is no theory of quantum gravity and it does not address the issues of dark matter and dark energy.

QUESTION:
If I place a liquid filled container on a scale and suspend a mass with greater density than the liquid within the liquid and then release the mass, will the scale register the full weight of the mass while the mass is in motion (falling) as compared to when the mass has settled on the bottom? Will the scale read the same while the mass is accelerating as when it has achieved terminal velocity?

ANSWER:
Your second question indicates that you understand the answer will be different depending on whether the falling mass is accelerating or not. The figure shows that the weights of the fluid and the container will act down on the scale. Now look at the falling object. In addition to its weight there are two upward forces, the buoyant force B and the drag force D ; these are both forces which the fluid exerts on the object. But Newton's third law says if the fluid exerts a force on the object, the object exerts an equal and opposite force on the fluid. Therefore the scale will read W _f+W _c+B+D. If the object is falling with constant speed, it is in equilibrium and so B+D=W _o and the scale reads the total weight of container, object, and fluid. If the object is accelerating down, B+D<W _o and the scale reads less than the total weight of container, object, and fluid. There is an earlier question similar to yours except the object is rising instead of sinking.

QUESTION:
Have scientists done experiment on what is the value of gravity below the earth surface as depth increases? if done pl. provide chart g vs depth.

ANSWER:
The deepest hole ever drilled is only about 12 km deep. I could not find any reference to attempts to measure g at various depths down this hole. Since the radius is about 6.4x10³ km, you would only expect about a 0.2% variation over that distance. There are models of the density of the earth, though, which have been determined by observing waves transmitted through the earth during earthquakes or nuclear bomb tests; these are believed to be a pretty good representation of the radial density and can be used to calculate g. The two figures above show the deduced density distribution and the calculated g.

Usually in introductory physics classes we talk about the earth as having constant density, but as you can see, that is far from true—the core is much more dense than the mantles and crust. If it were true, g would decrease linearly to zero inside the earth. Instead, it increases slightly first to around 10 m/s² and remains nearly constant until you are at a depth of around 2000 km. There is little likelihood that g will ever actually be measured deep inside the earth because the temperature increases greatly as you go deeper, already to near 200ºC at 12 km. However, if you have detailed information on density distribution, there is really no need to measure g.

QUESTION:
I'm so confused, my question is that if i hit the chair and chair change it's position from it's original position, then where is the reaction of chair and how according to third law of motion

ANSWER:
The force which you exert is on the chair. The reaction force is the force which the chair exerts on you. Only forces on the chair determine how the chair will move.

QUESTION:
I have a question thats driving me nuts. Say on a circle that spins, there are two points, one on the outer rim and one close to the rim. Both are in line with each other and are traveling at the same time but the distance of the point on the outside making one revolution is longer than the distance of the one on the inside. So the speed are the same but the distance of the inner point is shorter. The time they take to complete one rotation is also the same as the two points stay in line with each other. So speed is equal to distance divided by time as far as i know. Something have to give, don't understand it.

ANSWER:
The two points have the same angular speed but different translational speeds. For example, if the distance from the center is 1 m to the rim and 0.5 m to the other point, and the angular speed is 1 revolution/second, the distance traveled in one second is 2 π m for the rim and π m for the second point; the second point has half the speed (π m/s) of the first (2π m/s). Don't go nuts!

QUESTION:
Scientists say that centrifugal force is the only thing stronger than the pull of a black hole. What i want to know is what would happen if somehow the material around a black hole stopped spinning around it what would happen and how might the spinning be stopped?

ANSWER:
Funny, I never heard scientists say this. All that I can imagine you are thinking about is that in the right circumstances an object might orbit around a black hole just like the earth orbits around the sun without falling in. But, the black hole exerts such a large force that even light can orbit at a certain radius which is outside the Schwartzchild radius; inside the orbiting light, nothing with mass could have a stable orbit. See an earlier answer. Obviously, if you stopped this orbiting, anything would fall into the black hole.

QUESTION:
As part of our business we bag wrap passengers bags / suitcases prior to flying at the major UK airports. We use and have used for many years a power pre stretch cast film – 17 micron nano with a 300% capability. Recent feedback from Heathrow airport suggests some of the passengers bags are sticking to the conveyer belts and are being miss-directed. I am being asked for the "coefficient of friction" for the film we are using. I have advised our supplier of this, they have sent through the data spec sheet but there is no mention of COF, on speaking with them they have never had this question raised before. Personally, I do not think this Is an issue with our film but more where customers themselves are wrapping their own bags with home use film. However, I need to provide proof that the film we are using does not have any adhesive properties. My question is – would the COF affect this and how do I get the actual information on the film?

ANSWER:
The force of friction f depends on only two things: what the surfaces which are sliding on each other are (conveyer material and your plastic film) and the force N which presses the two surfaces together; normally, on a level surface, the force N is simply the weight of the object (suitcase in your case). There are two kinds of COFs, kinetic and static. The kinetic coefficient, μ _k, allows you to determine the frictional force on objects which are sliding. In that case, f=μ _k N. The static coefficient, μ _s, allows you to determine how hard you have to push on the suitcase in order for it to start sliding; in this case f _max=μ _s N where f _maxis the greatest frictional force you can get. Since you are being asked to prove that it is not too "sticky", it is the static, not the kinetic, coefficient which you need; measuring μ _sis quite easy. The only problem is that μ _sdepends on the surfaces so you must have a piece of the material from which the conveyer belts are made to make a measurement. Once you have that, use it as an incline on which to place a wrapped suitcase. Slowly increase the slope of the incline until the suitcase just begins to slide. Your COF (μ _s) is equal to the tangent of the angle of the incline which (see diagram above) is simply μ_s=H/L.

QUESTION:
I have a hill approximately 25 degree slope and 300 feet in length. Want to install a tow rope, what size of motor would I need at 240V, 3/4" rope and a 3 to 1 gear box. The anticipated speed is approximately 4 feet per second and at most I will have only two people on the tow rope at one time.

ANSWER:
I can only give you a rough answer. I will calculate the power needed to lift two large people (total mass 200 kg) up the hill. I will work in SI units because that is the system in which the watt is the unit of power. Your speed is v=4 ft/s=1.22 m/s so the rate at which the load is rising is vsin25⁰=0.516 m/s. The rate at which the energy of this mass is increasing is mgv=1011 J/s≈1 kW. I guess I would throw in a safety factor to account for friction and other energy losses, so maybe a 2 kW motor would do you. The voltage (240) and gear box are not really relevant in determining the power. Disclaimer: I am not an engineer, so you should get a second opinion!

QUESTION:
A 1500lb 8'x8' box that is 3'6" tall is lifted at one of the four side so that the opposite side acts as a pivot on the ground (like a strong man flipping a giant tire in a a world strongest man competition). How much actual weight is being lifted? assuming that the weight distribution of the box is perfectly even.

ANSWER:
Well, that depends on how you lift it. Let's assume that you lift it so that you cause it to rotate with uniform speed. One way that you could accomplish this is to push in a direction perpendicular a line drawn from where you are pushing and the edge on the box remaining on the floor. Referring to the figure above, the equilibrium conditions are N+Fcos θ-W=0, f-Fsinθ=0, and ½LW-LFcosθ=½W-Fcosθ=0; here F is the force you exert, W is the weight, N is the force the floor exerts vertically, and f is the frictional force exerted on the floor. Solving these I find that N=½W, F=½W/cosθ, and f=½Wtanθ. I suspect that the case you are interested in is when you first lift it off the ground, θ=0. F=750 lb, half the total weight. Note that this analysis is valid as long as the floor is not too smooth, that is the box does not start sliding at some angle; the angle is less than θ=tan^-1(L/H) because at that angle the center of gravity is directly over the pivot side.

Of course there are lots of other ways you could lift it which would be more efficient if your aim was to tip it over; for example, you could start pushing horizontally once you got it off the ground so that the floor would hold up all the weight rather than half the weight. There is an old answer very similar to yours that you might be interested in.

QUESTION:
I f a tennis ball and a football is thrown from a certain hieght then which ball will land first?

ANSWER:
I will assume that you do not mean an American football, rather a soccer ball. Also, it is not unambiguous what "…thrown from a certain height…" means. Imagine that we just drop each from some height. If air friction is ignored, they hit the ground simultaneously; this would approximately be the case if they were dropped from a few meters. However, air drag becomes more important as the speed increases. The drag force f may be approximated as f≈¼Av ² where A is the cross sectional area (πR ²) and v is the speed (you must use SI units). So, for a ball, f-mg=ma where m is the mass, a is the acceleration, and g is the acceleration due to gravity. Since f gets bigger as v gets bigger, eventually f=mg and the ball will stop accelerating and fall with a constant speed. The velocity at which this happens is called the terminal velocity v _t=√[4mg/(πR ²)]. The mass and radius of a tennis ball are m=0.059 kg and R=0.069 m; the mass and radius of a soccer ball are m=0.43 kg and R=0.22 m. So, I find v _t ^tennis≈50 m/s for the tennis ball and v _t ^soccer≈11 m/s for the soccer ball. The tennis ball will easily win the race because it continues accelerating long after the soccer ball stopped accelerating.

QUESTION:
I love hearing about new discoveries from particle accelerators, but one aspect of them confuses me. If we accelerate particles to 99% of the speed of light, shouldn't that make the matter appear to go slower to us, a la the twins paradox? Why don't these particles approach infinite mass and compress time from our perspective?

ANSWER:
Stable particles, those usually accelerated, do not carry clocks with them; but, if they did, those clocks would run slowly compared to yours. Some particles do carry clocks, those which are unstable. Suppose that the average lifetime of some particle were 1 s and its speed was 0.99c. You would observe it to live for 1/√(1-.99²)=7.1 s. The accelerated particles do indeed approach infinite mass but they have a really long way to go to get there even in the most powerful accelerators; see an earlier answer.

QUESTION:
My question relates to my own voluntary time involved with the rope/rigging community. It is not of any commercial interest to me, but the answer to my question has eluded me for a long time despite research and attempts to calculate it ! If you could at least explain to me the correct method of attempting to work our the answer I would greatly appreciate it. Question background - horizontal restraint line. A 7.6 m long horizontal rope is anchored at both ends. It is 2m horizontally above ground level (AGL). It is pre-tensioned to 50kg. A 20kg mass is suspended vertical above the horizontal rope and attached to the rope by a leash of 0.7 m length. The object/leash attachment point is mid-way along the 7.6 m horizontal rope i.e. 3.8 m from either anchor. The 20 kg object is then dropped. At the time of peak impact force, the sag in the horizontal tension line is 1.0 m. Despite my best efforts I do not seem to be able to calculate theoretical (i) peak impact forces on the anchors (ii) peak impact force on the object. I do however have peak impact force load cells that have recorded average (i) peak impact forces on the anchor 220 kg and (ii) peak impact force on the object 115 kg. Is it possible for you to detail the correct formula/method for at least working the theoretical approach to calculating these forces ?

QUERY:
It would be helpful if you could tell me the sag and forces when the mass is hanging at rest on its leash. I take it that the 115 kg measurement is the tension in the leash.

REPLY :

ANSWER:
Let me first try to understand the data for the "loads" (essentially the tension in the rope, T , and the tension in the leash, F ) in terms of simple physics; then I will try to generalize it. Normally, physicists do not like to use kg to measure force, but I will go ahead and do that here. Focusing on the point where the leash is tied to the rope, the force which the rope pulls up is 2Tsinθ=F. In the case of the hanging mass, sin θ=s/ √(L ²+s ²)=0.41/√(3.8²+0.41²)=0.11, so F=20=0.22T; thus T=91 kg which is in reasonable agreement with the measured value of 100 kg. In the case of the maximum s, sin θ=0.25 and F=0.51T. Taking the measured value of F=115 kg, T=225 kg, again in good agreement with the measured value of T=220 kg.

At this point what a physicist normally does is to try to understand the situation in terms of a simple spring model. If the rope is like a simple spring, i.e. its tension is proportional to its stretch, you can usually make approximations which would result in the simple model that F≈ks where k is a constant. For the equilibrium situation, then, 20≈0.41k or k≈49 kg/m. This would then predict that the force when s=1 m would be F=49 kg which is too small by more than a factor of 2.

The previous try indicates that the rope is probably not approximated as an ideal spring. My last attempt is to try to treat the rope more explicitly as an ideal spring, not using small approximations used above. So, looking at one half the rope, I will write T=50+kδ where δ=√(L ²+s ²)-L is the amount by which this half of the rope is stretched relative to L. Note that k is not the same as in the approximation above where s was the stretch parameter rather than δ. Calculating δ for the at rest situation where T=100 kg, k=2270 kg/m. Then, calculating T for the maximum s using this value of k, T=50+2270x0.129=344 kg which is too large by nearly 60% compared to the measured value of 220.

I conclude that the rope is poorly approximated as an ideal spring and that to do any more detailed analysis of this problem would require measuring s as a function of the load by varying the load for the equilibrium situations.

FOLLOWUP QUESTION :
If possible, without the aid of the load cell values which I get by practically performing the drop test. How would you derive the theoretical values for the tension/force at the both the anchor and on the body in the drop test scenario. I understand how to calculate forces etc for the system at rest, but it is the dynamic falling system, deceleration etc that I am unable to clarify. To summarise, if you have the load/object, placed at any height above or below the horizontal line (depending on the leash length), without loading the horizontal line, and then you drop the object, what would be the correct formula method to determine the approximate theoretical peak impact forces on the anchors and body, without the luxury of any load cell info. when it comes to rest after being decelerated by the horizontal line.

ANSWER:
You apparently did not understand my answer, particularly the second and third paragraphs. The first paragraph shows that the data are consistent with the simple model for the tensions in the ropes. I found these very encouraging. From the data for the dynamic point you could, of course, calculate the acceleration of the weight at that point. 20a=(115-20)g so a=4.75g=46.6 m/s².

Then I tried to model the rope as a simple spring, the tension is proportional to the stretch. I failed to do so in both attempts. You do not know the force which this rope will exert given a certain amount of stretch. Physics may be powerful, but you cannot do any predictive calculation if you are ignorant of the force. I have two data points but that is not enough if the force is not linear. The last paragraph suggests the only hope for having a predictive analysis: you need to measure the tension in the rope as a function of what you call sag. To do this you need to use many weights, say at 2 kg steps, and measure load#1 and sag. This would give me the information necessary to do predictive calculations. Life in the real world is not always simple and analytical. It occurs to me you do not really need to hang varying weights because you have the load#2 device; just pull down on it until it reads 2 kg, 4 kg, 6 kg, etc.

It is, of course, simple to calculate the speed the weight has just before the leash goes taught: v=√(2gh) where is the distance fallen.

QUESTION:
A conductor, even though it is carrying a current, has zero net charge. why then does a magnetic field exert a force on it?

ANSWER:
Magnetic fields exert forces on moving charges. In the conductor, negative charges are moving but positive charges are not. A magnetic field exerts no force on charges at rest.

QUESTION:
Do all five balls on a Newton's Cradle have to weigh the exact same amount in order for it work correctly?

ANSWER:
No. The balls on the ends need to be the same mass. However, you could no longer do the demonstration where if you send 2, 3, or 4 balls in that there would be 2, 3, or 4 balls out.

QUESTION:
If F=Q1.Q1/R^2, does it mean that two unlike charges touching each other have infinite forces of attraction between each other? If so, how are we able to separate 2 oppositely charges objects which are stuck together with our bare hands?

ANSWER:
As often happens, you are applying an equation (Coulomb's law) without asking whether it applies. This law is true for two point charges or for two spherically-symmetric charge distributions; in the second case, R is the distance between the centers of the spheres. So, if you have two charged insulating spheres of radii 1 cm and 2 cm which are touching, R=3 cm.

QUESTION:
What is inertia? From what I understand, the inertia for a sphere is: I = (2/5)MR^2. Why is the radius included? Why is the volume of the sphere related to the resistance to change motion? As long as any 2 objects have the same mass, why should they have different inertias?

ANSWER:
Inertia means the inherant ability of something to resist being accelerated. There are two kinds of acceleration, translational acceleration a (like a car speeding up or slowing down), and rotational acceleration α like the rotational speed of an engine's flywheel speeding up or slowing down. Inertia for resisting a is simply mass which you can see from Newton's second law, a=F/m. If you double the mass on which a given force acts, you halve the acceleration; mass is sometimes called inertial mass for this reason. For rotational acceleration, the rotational inertia depends not just on how much mass there is, it also depends on how it is distributed; for example, it requires much more effort to get a wheel with radius 1 m spinning than it does to spin a wheel with the same mass but a much smaller radius. The rotational form of Newton's second law is α=τ/I where τ is the torque applied to the object whose moment of inertia is I. In rotational physics torque plays the role of force and moment of inertia plays the role of mass.

QUESTION:
If friction acts perpendicular to the direction of motion, if i place an object against a wall and let go, since the object is falling downwards, will friction from the wall cause the object to move away from the wall? Also if I am standing still, gravity results in a downwards force so friction should act leftwards or rightwards. Which one is the correct one (assuming that i am not moving)?

ANSWER:
Friction does not act perpendicular to the direction of the motion but opposite it. When the surface is vertical there is no frictional force. This ignores irregularities in the wall and air drag. If you are standing on a horizontal surface and not moving, the frictional force on you from the floor is zero.

QUESTION:
I am an engineer working on the reconstruction of a traffic accident where it is alleged that a car traveling over a railroad crossing became airborne at a speed lower than the posted speed of the road. The information that I have available includes the type and make of the car and the geometry of the road. Nothing in the engineering literature that I can find addresses this issue. Despite the five quarters of physics that I took long ago, I am having trouble finding the information that I need to model this. Any suggestions?

ANSWER:
This is sort of a classic introductory physics problem. The idea is: when does an object lose contact with the surface on which it is moving, usually taken to be a segment of a circle. I will do an approximation that the shape is a circle and that the car is a point mass. You can then generalize to your case from there or else give me more information. In the sketch above, the radius of the circle is R, the weight of the car is mg, the angle specifying the current position of the car is θ, the force which is causing the car to move with some constant speed v is F, and the normal force of the road on the car is N. Note that although the car has a constant speed, it has a centripetal acceleration a=v ²/R toward the center of the circle. Applying Newton's laws, F-mgcosθ=0 and mgsinθ-N=mv ²/R. The first equation tells you what force you need to keep it moving at a constant speed, F=mgcosθ which is really not of interest to you; note that the force is in the direction of v on the way up and opposite on the way down since the cosine changes sign at 90⁰. The second equation tells you what N is for any position of the car, N=mgsinθ-mv²/R; note that if N is negative it points toward the center but the road cannot pull down, only push up, so the car could not stay on the road at that speed and angle. What is really of interest is under what conditions would N=0=gsinθ-v²/R or v ² =Rgsinθ; this would tell you the speed (angle) at which a car with a particular angle (speed) would leave the road. Note that it is independent of the mass. Notice also that v ²/Rg<1 because the sine function cannot be larger than 1.0. For example, for what speed will the car leave the road at 45⁰ if gR=300 (m/s)² (R≈30 m)? v=√(300x0.707)=14.6 m/s=32.7 mph. Or, at what angle will a car with speed 35 mph=15.6 m/s leave the road? θ=arcsin(15.6²/300)=54.2⁰.

One thing which occurs to me though is, since you know the car and railroad crossing, why don't you just do the experiment and drive it over the crossing?

QUESTION:
When i place an object in between my 2 palms, why does it not fall? My palms only supply horizontal force, where does the vertical force come from to hold the object between my palms without falling?

ANSWER:
You are wrong to say that your "…palms only supply a horizontal force…" When surfaces are in contact, the forces they exert on each other have components both perpendicular (normal) and parallel (friction) to the surfaces. It is the friction which holds the object. If the object were very heavy, say 100 lb, and your hands were greased, you would not be able to hold it up because the frictional forces would not be as large as the weight.

QUESTION:
Say there is a cylinder on a ramp and the friction force from the ramp cancels out the parallel component of gravity. Therefore, the cylinder should be in linear equilibrium. However, from the reference point of the center axis of the cylinder, there is a net torque exerted by the friction force. Additionally, there is also a net torque exerted by the gravitational force from the reference point of the point of contact of the cylinder and the ramp. Therefore, it is not in rotational equilibrium and should start to rotate, correct? How is this possible, because if the cylinder starts to roll how can it also be in linear equilibrium?

ANSWER:
There is a simple answer to your question: the frictional force is not equal to the component of the weight along the incline. Rather, -f+mgsin θ=ma where θ is the angle of the incline and a is the acceleration of the center of mass down the incline.

FOLLOWUP QUESTION:
Thank you very much for your response. However, I think you may have misunderstood my question. I was asking what would happen in a case where the frictional force is set to cancel out the parallel component of weight. It seems as if the center of mass cannot move, but the cylinder needs to rotate. Therefore, it would appear as if the only outcome of this situation would be a cylinder rotating in place on a ramp, which does not seem possible. I think that the cylinder would have to roll down the ramp, but I can't see how this would be consistent with linear equilibrium.

ANSWER:
I did not misunderstand your question. You cannot simply adjust the friction to be what you want it to be. You can, however, simulate what you want to happen by wrapping a string around the cylinder and pulling up on the string with a force mg sin θ where θ is the angle of the incline and m is the mass of the cylinder; imagine that the incline is smooth (frictionless). Now there will be a net torque about the center of mass of mgRsinθ=Iα where I is the moment of inertia and α is the angular acceleration of the cylinder. The cylinder will spin in place. Your hand will have an acceleration of a=mgR ²sinθ/I; for a uniform solid cylinder with I=½mR ², a=2gsinθ.

ADDED THOUGHT:
If the coefficient of kinetic friction is exactly equal to μ _k = tan θ, the cylinder will slide down the incline with constant speed because the frictional force will be f=μ _k N=(tanθ)(mgcosθ)=mgsinθ. So, if you start it sliding and not rolling, it will begin spinning about its center of mass because of the torque due to the friction and have an angular acceleration α=fR/I; it will continue sliding down the plane with constant speed, though.

FOLLOWUP QUESTION:
Thanks again but I am still a bit confused. It makes sense that the center of mass will move at a constant velocity while the cylinder is rolling, but how did it acquire that velocity in the first place if I start the cylinder at rest and not sliding as you wrote in the additional thought. In other words, what happens if the coefficient of static friction is equal to mgsinθ and the cylinder starts with no velocity of any kind?

ANSWER:
If you start the cylinder at rest on the incline and μ _k = tan θ (coefficient of static friction will be larger), the cylinder will roll without slipping. If you solve the dynamics for the cylinder rolling without slipping you will find that (see the figure above) f=(mgsinθ)/3 and a=(2gsinθ)/3 where f is the frictional force and a is the acceleration of the center of mass. Since f<mgsinθ, if you simply let it go, it will roll without slipping. So, if you want it to slide down with constant speed, you must give it a shove to start it slipping.

QUESTION:
Does mass of an object increase its mass exponentially as it approaches infinitely close to the speed of light?

ANSWER:
If df/dq=Aq for some function f(q), where A is a positive constant, f is said to be exponentially increasing with q. For your question, f is m and q is v. The expression for m(v) is m=m ₀/√[1-v ²/c ²] where m ₀ is the rest mass. Calculating the derivative, dm/dv=mv/[c ²-v ²]. Thus, although m increases without bound as v increases, it does not increase exponentially.

QUESTION:
Can sustaining enough angular momentum help us stay in a black hole for longer(near the event horizon)? If yes, how much energy would be required to sustain it for ten minutes.

ANSWER:
What do you mean by "in a black hole"? A black hole is a singularity so if you were "in" it you could not have any angular momentum. In any case, I am assuming that your idea is to orbit the black hole so as not to fall in. If you were able to do this, no energy would be required; the earth orbits the sun in a stable orbit with no energy input. However, it is not possible for any object to orbit a black hole anywhere near the Scwartzschild radius because the speed would be too large. At a radius of 1.5 the Schwartzschild radius, light would orbit a black hole in a circular orbit (see earlier answer). This is a result of general relativity. No stable orbits inside this exist and anything inside would fall into the black hole.

QUESTION:
Hi! I have been told that hypothetically speaking when a metal bar or something other object travels in space at the speed of light it shrinks. So my question is if it is correct and why yes or no?

ANSWER:
First of all, nothing can travel at the speed of light. However, the fact that moving lengths are shorter is not hypothetical, it is simple fact which has been verified by measurements. It is the result of the special theory of relativity. And, it is not because they appear to be shorter, they actually are shorter. You might look at an earlier answer about length contraction.

QUESTION:
We have material that generates electricity when exposed to light, or force. Why haven't not found one that does this when exposed to atomic radiation. Imagine almost permanent batteries.

ANSWER:
There are batteries which get their primary energy from radioactive decay. Atomic batteries are routinely used in heart pacemakers and low-power requirements in space probes.

QUESTION:
My question is about the theory of relativity and time dilation. It appears to only work in one direction and I'm not sure why. For example, take a person on earth and compare to a person in a rocket going near the speed of light. The person on earth observes the rocket man going near light speed and aging slower. The man in the rocket observes earth moving past him near the speed of light except the earth man ages quicker.

ANSWER:
Congratulations, you have discovered the twin paradox! It is true that the earth man's clock runs slow in the rocket man's frame. It also is true that the rocket man's clock runs slow in the earth man's frame. But to make a definitive comparison, they must somehow bring their clocks together to compare. In other words, the rocket man has to come back to compare his clock with the earth-bound clock. To get the full explanation of the twin paradox, look on the faq page.

QUESTION:
Can a ball bounce higher than the height it was dropped? I know that air resistance would slow it down but is it possible?

ANSWER:
Even if you bounced a ball in a vacuum where there would be no air resistance, it could not bounce higher than the height from which you dropped it. The only way to achieve this would be to add more energy to the ball, either throw it down rather than drop it or maybe have a little "kick" from its interaction with the floor.

QUESTION:
An ice-hockey player throws his stick on the ice. The stick translates and rotates. Before it stops, it always rotates and translates - never only rotates or translates. Why do both motions occur simultaneously like this?

ANSWER:
It actually depends on how it is thrown

FOLLOWUP QUESTION:
S uppose it isn't thrown intentionally in such a way so as to just make it spin or just make it translate.

ANSWER:
The motion of a rigid body moving in two dimensions (the ice, call it the x-y plane) may be broken into two components, motion of the center of mass (translation) and motion about the center of mass (rotation). There are, in your example, no forces in the x- or y-direction once the stick has been thrown if you neglect friction. If the force you throw it with is directed through the center of mass, it will not rotate because there is no torque about the center of mass to get it rotating. If the net force you throw it with is zero (you would need to use two hands to do this) it will not translate. If you just randomly grabbed it and threw it, there would be a net force which would result in the center of mass accelerating during the time you were throwing it; and there would be a net torque which would result in the stick having a rotational acceleration during the time you were throwing it. Once you let go, there is no force and no torque on the stick and so both linear and angular momentum would be conserved meaning it would continue moving the way it was moving when you released it.

QUESTION:
Suppose a container full of water is kept in a certain area. Let no external force be applied. Now the question is: Will there be an overall circulation of molecules of water? Or will the rest position of water perfectly 100% at rest?

ANSWER:
There is a difference between no "circulation of molecules" and "100% at rest." The molecules in a glass of water are never at rest, they are always moving around. However, in a glass which has been sitting undisturbed for a long time the average velocity is zero, there are always as many moving in any direction as there are moving in the opposite direction. However, you could have a fluid which has a zero average velocity of molecules but they could be circulating (like a whirlpool). If you start such a circulation, it will often last for a relatively long time but, due to viscosity and fluid drag forces, it will eventually die out.

QUESTION:
This is a brain teaser I have been having trouble with. Lets say a clock is moving towards me at a 50% of the speed of light. When the clock is moving towards me, do I observe its hands to be ticking slower, faster, or at the same rate compared to the rate of ticks that I observe when it's moving away from me?

ANSWER:
A clock will appear to run faster than yours when moving toward you. A clock will appear to run slower than yours when moving away from you. But that clock is actually running more slowly than yours in both directions (and not by the same factor as it appears to run when going away from you). I think you will understand why is you look at earlier answers to a particular faq on the faq page. Keep in mind that moving clocks run slow, they do not just appear to run slow; how things are and how things seem are often not the same.

QUESTION:
Many Science Fiction ships have for protection a shield that stops projectiles and saves the ship from a lethal impact. Such an example would be the energy shields possessed by the faction known as Covenant from Halo. So given the laws of Newton and the third law about there always being an equal force countering the force that was exerted first, wouldn't this just mean that whenever the energy shield takes a hit by a projectile, the force would ''travel'' from the shield to whatever generator generates the shield. Like the UNSC Frigates shoot a 600 ton slug at 30km/s. They're 30ft long and around 7ft wide. So they have a lot of force and momentum behind them. So wouldn't an impact like this just cause the shield generator to be violently thrown off its attachments and ''fly off'' through the compartments of the ship destroying a lot of the ship?

ANSWER:
"So they have a lot of force and momentum behind them." Yes, these projectiles have a lot of momentum, but saying that "…there is a lot of force…behind them…" has no meaning. The momentum a slug has is p=mv=(6x10⁵ kg)(3x10⁴ m/s)=1.8x10¹⁰ kg m/s. When this hits something, it will certainly exert a force, but the magnitude of that force will depend on how long it took to stop. I have no idea how big it is, but suppose it has a radius of 10 km from the ship; I will think of it as very flexible and suppose that it stretches inward just stopping before it hits the ship. I also will assume that the ship is much more massive than the slug; (elsewise how could a comparably-sized ship carry a bunch of them and fire them without huge recoil?) If it stops in 10 km=10⁴ m with uniform acceleration, I can apply simple kinematics, -3x10⁴ =at and 10⁴=3x10⁴+½at ², and find that t=1.5 s, the time for the slug to stop. The average force felt by the slug is (Newton's second law) the rate of change of the momentum, F=1.8x10¹⁰/1.5=1.2x10¹⁰ N. You are certainly right, this very large force will be felt by the ship because of Newton's third law. But suppose that the ship is 100,000 times more massive than the slug, 6x10¹⁰kg; in that case, the final velocity of the ship after being hit will be found from F=mv/t=6x10¹⁰ v/ 1.5=1.2x10¹⁰ N, so v=0.3 m/s, not so bad! If the shield were very rigid, it would be catastrophe for the ship. I have never played these games but I expect the shield is shown as stopping the slug almost instantly.

A little should be said about the other end, launching the slug in the first place. In this case, unless the cannon has a 10 km barrel, the recoil force on the ship will be huge. You would be interested in similar Q&As along the same line as yours.

QUESTION:
If I were to drop two round balls of different mass under water would they both fall to the bottom at the same velocity or would one reach the bottom first?

ANSWER:
The forces on a ball are its own weight mg down; the buoyant force B up which would be equal in magnitude to the weight of an equal volume of water; and the drag force f up which would depend on the size the ball and its speed. The net force F would be F=-mg+B+f; as the ball went faster and faster, f would get bigger and bigger until eventually F=0 and the ball would go down with a constant speed called the terminal velocity. The larger the mass, the larger the terminal velocity. Without specifying the the sizes of the balls, your question cannot be answered. If they had identical sizes, the heavier ball would reach the bottom first because it would have a larger terminal velocity. Of course, if B>mg the ball would float!

QUESTION:
If you performed the double slit experiment in outer space and were observing the electron particles would you get a diffraction pattern or two rows of particles. Does the earth's atmosphere have any effect on the experiment?

ANSWER:
Any electron diffraction experiment is always performed in a vacuum. The range of the electrons in air is short enough that it would entirely ruin any experiment you tried to do. Electrons interact strongly with any atoms in their vicinity. In outer space you would have a vacuum so you would see a diffraction pattern.

QUESTION:
I'm trying to find a fast/easy way to test whether a sealed, consistently-dimensioned rectangular box is sufficiently "stable" for transport on a (small) 2-wheeled bicycle trailer. The box is pretty tall. If it's over-weighted and top-heavy, it'll flip the trailer around turns (which are sufficiently tight/quick). I figure there might be a quick, static "tip test" with a combination pull gauge, inclinometer and scale, but my math skills are primitive. Is there a simple way to ascertain whether, for a given object, a target stability threshold is met?

ANSWER:
There is an earlier answer about a bicycle making a turn. It would be helpful for you to read that first. The easiest way to do this problem of your trailer turning a curve is to introduce a fictitious centrifugal force which I will call C , pointed away from the center of the circle; the magnitude of this force will be mv ²/R where m is the mass of the box plus trailer, v is its speed, and R is the radius of the curve. The picture above shows all the forces on the box plus trailer: W is the weight and the green x is the center of gravity (COG) of the box plus trailer; f ₁ and f ₂ are the frictional forces exerted by the road on the inside and outside wheels respectively; N ₁ and N ₂ are the normal forces exerted by the road on the inside and outside wheels respectively; the center of gravity of the box plus trailer is a distance H above the road and the wheel base is 2L (with the center of gravity halfway between the wheels). Newton's equations yield:

f ₁+f ₁=C for equilibrium of horizontal forces;
N ₁+N ₂=W for equilibrium of vertical forces;
CH+L(N ₁-N ₂)=0 for equilibrium of torques about the red x.

If you work this out, you find the normal forces which are indicative of the weight the wheels support: N ₁=½(W-C(H/L)) and N ₂=½(W+C(H/L)). A few things to note are:

the outer wheel supports more weight,
if C=0 (you are not turning), the inner and outer wheels each support half the weight,
at a high enough speed C will become so large that N ₁=0 and if you go any faster you will tip over, and
if the road cannot provide enough friction you will skid before you will tip over.

Now we come to your question. You first want the maximum speed without tipping. Solving for v in the N ₁=0 equation gives

v _max =√[RWL/(mH)]=√[RgL/H]

where g=9.8 m/s²=32 ft/s² is the acceleration due to gravity. For example, suppose that R=7 ft, L=17 in=1.42 ft, H=30 in=2.5 ft. Then v _max =√[7x32x1.42/(2.5)]=11.3 ft/s=7.7 mph.

Be sure to note that the assumptions of a level road (not banked) and wheels not slipping are used in my calculations. Also be sure to note that W is the weight of both box and trailer and 2L is the wheel base, not the box width.

One more thing is that you might not know how to find the COG of the trailer plus box. If the COG of the trailer is H _trailerabove the ground (probably close to the axle) and the COG of the box is H _box above the ground, then H=(H _boxxW _box +H _trailerxW _{_trailer})/W.

ADDED THOUGHT:
When just about to tip, all the weight is on the outer wheel and so N ₂ =W and f ₂=μN ₂=μW, where μ is the coefficient of static friction. If you work it out, the minimum value the μ must have to keep the trailer from skidding is μ _min =L/H. For the example worked out above, μ _min =0.57. For comparison, μ for rubber on dry asphalt is about 0.9, so the trailer would not skid.

QUESTION:
If a 20 pound rock and 100 pound rock or drop from 1000 feet which will hit the ground first.

ANSWER:
If air drag is neglected, they would hit simultaneously. If air drag is considered, it would depend on the geometry of the two objects. If they have identical shapes and sizes, the heavier rock would hit first; otherwise, you would need to know the shape and size of each to calculate the times to fall. See the faq page.

QUESTION:
A starship pilot wants to set her spaceship to light speed but the crew and passengers can only endure a force up to 1.2 times their weight. Assuming the pilot can maintain a constant rate of acceleration, what is the minimum time she can safely achieve light speed?

ANSWER:
This question completely ignores special relativity. It is impossible to go as fast as the speed of light. Furthermore, acceleration is not really a useful quantity in special relativity and you must use special relativity when speeds become comparable to the speed of light. I have earlier worked out the velocity of something which would correspond to occupants of your spaceship experiencing a force equal to their own weight due to the acceleration which I will adapt to your case later. (See the graph above.) First, though, I will work out the (incorrect) Newtonian calculation which is presumably what you want. The appropriate equation would be v=at where v=3x10⁸ m/s, a=1.2g=11.8 m/s², and t is the time to reach v; the solution is 2.5x10⁷ s=0.79 years. For the correct calculation, you cannot reach the speed of light; from the graph above (black curve), though, you can see that you would reach more than 99% of c when gt/c=3. To make this your problem, we simply replace g by 1.2g and solve for t. I find that t=7.7x10⁷ s=2.4 years.

QUESTION:
Why do wavefunctions need to be normalized?

ANSWER:
So that the absolute square of the wave function can be interpreted as a probability density. The integral of ψ*ψ over all space is then the probability of finding the particle somewhere which, of course, must be 1.

QUESTION:
Will a heavier ball roll down a small slope faster than a lighter ball? Or will a lighter ball roll down a small slope faster than a heavier ball?

ANSWER:
If both are solid balls of the same radius but of different masses, they will take equal times if air drag is neglected as might be appropriate for a "small slope". If they get going fast enough that air drag becomes important, the heavier ball will win the race.

QUESTION:
During refraction why does a light ray bend...and how we can account for conservation of momentum?

ANSWER:
This is not simple. See this article.

QUESTION:
The following situation occured with my son, would you mind sending me the formula or the resulting impact force? Car A 1430kg rear-ends car B 1143 kg. Car B (Automatic gear is on park) is shoved 2 meters (6.56168 feet) before stop. What is the impact force on Car B Tons?

ANSWER:
No way to calculate this without much more information. See the FAQ page for other impossible to calculate the force situations.

FOLLOWUP QUESTION:
Thank you very much for your reply. I went to your site faq and understand what you mean (speed + stop time), but on this site it gives me force on the car 7. Tones with just the weight of car one and 2 meters of course it refers to 1 car hitting a tree, but the force of impact must be close. Does it sound reasonable to you?

ANSWER:
Maybe I could make a very rough estimate if I knew whether the incoming car was skidding, if the pavement was dry asphalt, was there any notable compression of the cars (like a bumper moved in by 2 cm)? Would a speed of about 15 mph be reasonable?

FOLLOWUP QUESTION:
Thank you very much for tryng to help find the force of impact. It was a mass pile up 6 cars (cars 1 to 4 Totalled) 01 Car 1950kg (estimated speed 55/60mph) ->02 Car 1172kg no brakes->(((Car 03 A 1430kg no brakes ->Car 04 B 1143 kg in Park gear)))->C 05 1270Kg (+ 4 occupants +- 280Kg no brakes)-> Shoved 1 meter to Car 06 Irrelevant - To simplify the calculations I reduced it to Car A and Car B - It was on dry asphat. The incoming (A) car was shoved 1meter (neutral gear no brakes) before hitting B and Car B in Park was shoved 2 meters into Car C which was shoved 1 meter into Car D - B car rear bumper was compressed by 25cm (lower body frame steel bent 10cm) - The estimated speed 25 mph of impact (Car 03 A to Car 04 B)

ANSWER:
Good grief! If I understand things correctly, it really is impossible now to do any meaningful calculations. I had thought from your earlier question that car B was at rest after going 2 m but now there are far too many unknowns. With two cars there was a possibility that I could have done a very rough estimate, with this situation it is truly hopeless. There is no reasonable way to estimate car A's speed or car B's speed after 2 m.

FOLLOWUP QUESTION:
Yep. That's why I simplified it to 2 cars. According to the lady in car A 1430kg she thinks her car was travelling at about 40Km / (I would say 25 miles) and shoved car B 1143 kg for 2.5 meter until it stop. (Stop means B hit C but this is irrelavant to a rough estimate) Dry asphalt Car B 25 cm rear bumper compression Without making it complicated with the compounded forces from other cars etc, all I would like to have a rough idea is, what aproximatly was the force of impact exerted from Car A onto car B. Do you that is possible to roughly calculate the force of impact Tons?

ANSWER:
OK, I give in! It is not irrelevant that car B was moving when it hit car C, but we can make a rough estimate now that I have the speed of A and the compression of the damage on B without any information about after the collision. I will assume that the time of the collision (compression of 25 cm=0.25 m) is very short so that I can ignore friction of the road, the collision is perfectly inelastic (A and B stick together), the speed of car A was 40 km/hr=11 m/s, and the compression of car B is negligible. Because this is a very rough estimate, I will retain only two significant figures throughout. Then the speed v after the collision has finished of the cars may be estimated from momentum conservation: 1400x11=(1400+1100)v, so v=6.2 m/s. The average force on car B is the rate of change in its momentum F=(6.2x1100)/t=6800/t where t is the time of the collision. Since we know the acceleration a is 6.2/t, we can use the kinematic equation for distance to get the time: 0.25=½at ²=3.1t, so the time of collision is t=0.081 s; therefore F=84,000 N=19,000 lb=8.5 ton.

QUESTION:
Why must the trajectory of the reduced-gravity airplane to be parabolic. Why not arc of the circle or anything else?

ANSWER:
The reason is that the path a projectile follows is a parabola. If you were in an airplane and it suddenly disappeared, you would follow a parabolic path determined by what your velocity was when the plane disappeared. So, if the plane flies to follow that path, you would be in free fall. For more information about this, see an earlier answer.

QUESTION:
I am writing a blog and had my friends to ask of what they would want to talk about.. I get this one. I have no clue with physics, so, I am asking. Explain why a photon particle- which is a very small bundle of energy and travels at the speed of light- seems to defy the laws of physics by never losing speed or velocity?

ANSWER:
There is no law of physics which says an object naturally loses velocity. To change the velocity of something you have to apply a force to it, it must interact with something. If you had a bowling ball which had no forces on it it would continue going with a constant speed in a straight line forever. This is just Newton's first law. However, Newtonian mechanics is not valid for a photon, but it behaves like any other particle when it experiences no interactions which would change it. There is one important difference—regardless of how it interacts with something else, it never speeds up nor slows down; the speed of light in a vacuum is a constant of nature. If you look on my faq page you will find links to discussions regarding why the speed is constant and why it has the value it does. When you throw a ball up in the air, it slows down; you throw it down from a tall building, it speeds up. Photons don't do that but they do change their energies by changing to a longer, redder (shorter, bluer) wavelength when going up (down) in a gravitational field.

QUESTION:
Gasoline contains 40 megajoules of energy per kilogram and gasoline trucks have around a hundred tons of it. So how does a gasoline truck exploding not produce an explosion similar to a small nuke?

ANSWER:
Since it is always a little ambigous what is meant by a ton, I did my own calculation using the volume of a tanker truck of about 10,000 gallons and the density of gasoline of about 2.7 kg/gallon. I got the total energy content of about 10¹²J. The energy of the Nagasaki bomb, a small bomb by today's standards, was about 10¹⁴ J, 100 times bigger. Two things to consider are:

T he bomb number represents total energy delivered whereas I would guess that likely less than half the energy content of the gasoline would actually be delivered.
The time over which the energy is delivered is likely much longer for the gasoline explosion than the nuclear explosion. As an example, just to illustrate the importance, suppose the bomb exploded in 1 ms=10^-3 s and the tank in 1 s. Then the power delivered by each is 10⁸ GW for the bomb and 10³ GW for the tank. As a result the destructive power of the bomb would be much bigger.

QUESTION: Centrifugal force seems so much confusing to me. I read on the books that centripetal and centrifugal force never act on the same object (Halliday-Resnicks' "physics" and several of our intermediate text books) and centrifugal force never acts on the moving object. But in many cases (effects of earth's rotation on g, roller coaster's loop etc) the centrifugal force are said to act on the moving object (as our text books say!). So what's right and what centrifugal force actually is?

ANSWER:
Newton's laws are true only in what we call an inertial frame of reference. Any frame which is accelerating is not an inertial frame of reference. Here is an example: suppose you are in a car going 80 mph and the driver slams on the brakes. If you are not wearing your seatbelt, you suddenly experience an acceleration toward the windshield. But, there are no forces on you which suddenly impel you forward, so Newton's first law is false for you because you are accelerating in your frame even though there are no forces on you. Of course someone watching this from the roadside has no problem understanding what is happening: because there are no forces on you, you continue moving forward with a constant speed while the car is stopping. There is a very neat trick you can use to make Newton's laws work in an accelerating frame: you just add a force which is the negative of the acceleration of the frame times the mass of the object you are calculating; such a force does not really exist and we call it a fictitious force. So, for you in the accelerating car we add a force, let's call it the "impulsive force" in the forward direction, which is your mass times the magnitude of the car's acceleration. You can then say that you accelerate forward with the same acceleration as the car is accelerating backward because you are being pushed by the impulsive force.

Centrifugal force is a fictitious force. If you are on a merry-go-round you feel a force trying to push you off; there is no such force. But if you pretend there is, you can do use Newton's first law: there is a centrifugal force outward which is mv ²/R and you are at rest; the force which is keeping you from accelerating outward is friction with the floor, so it must be equal to mv ²/R. If someone on the outside analyzes the problem she will say that you have an acceleration v ²/R inward so there must be a force (centripetal) inward to provide that acceleration, F=mv ²/R which is the same frictional force we found on the merry-go-round. Clearly the centrifugal and centripetal forces in these two cases are acting on the same body—you—so your claim that texts say otherwise is strange. In 40 years of teaching I have never heard such a claim. It is true that both centripetal and centrifugal forces never act in the same solution to a problem; if you choose a person on the merry-go-round to analyze, you never have both a centripetal and centrifugal force acting on that person. Perhaps you misunderstood and that is what is meant by never acting on the same object.

You can learn more about fictitious forces in an earlier answer and the links it leads to.

QUESTION: Two balloons, one with He gas is attached to the lower part of car and one with ordinary air is attached to roof hanging downward. When brakes are applied in what direction both balloons will move?

ANSWER:
The helium balloon will move backward; see an earlier answer for an explanation. (Note that the earlier answer has acceleration rather than braking.) The air balloon will move forward because it feels no buoyant force and therefore its inertia will cause it to want to crash into the windshield.

QUESTION: If a man could travel with a near speed of light, what would happen to him if he'd run though an elephant. Would that man be demolished or could he survive that impact?

ANSWER:
Are you kidding? A man going 200 mph, far below the speed of light, would be instantly killed in this scenario. A 100 kg man going at 80% the speed of light would bring in about 5x10¹⁸ J of energy to the collision which is equivalent to about 10,000 Nagasaki atomic bombs. Not only would the man and elephant be obliterated, also anything within miles would be.

QUESTION:

What exactly is momentum and how is it different from force?
I understand that p = mv and F = ma but they seem so similar in application that I haven't fully wrapped my head around it.
Additionally, what does it mean for something to have momentum in the first place, and why must it be conserved?
How does light have momentum if it, by nature, has 0 mass (I presume E =mc^2 comes into play somewhere here)?
Finally, what is the significance in the fact that light does have momentum (if it does)?

ANSWER:
You have lots of questions, really. I have rearranged your question to delineate it into parts:

For your first question, just say that p=mv. My answer to #2 should clarify how force and linear momentum are related. Force and momentum have to be different because they are not even measured in the same units—momentum is mass*length/time and force is mass*length/time².
What is acceleration? It is rate of change of velocity, a=(v ₂-v ₁)/t where t is the time to change speed from v ₁ to v ₂. So one could write that F=(mv ₂-mv ₁)/t=(p ₂-p ₁)/t; so force may be thought of as the rate of change of momentum. Newton actually stated his second law this way, not as F=ma. It is the second law which is a fundamental law of physics, momentum is just defined because of its simple and natural relationship to the second law.
It doesn't "mean" anything for something to have momentum, it is just a definition. However, consider the second law if there is no force acting; then F=0=(p ₂-p ₁)/t. In other words, p ₂=p ₁which simply means that momentum does not change (is conserved). The condition for conservation of momentum of a system is that there be no external forces on it. For example; suppose you look at an isolated galaxy which has billions of stars in it all interacting with each other and there are negligible forces from the outside; if you sum up all the momenta of all the stars today and in 10 years from now, you would get the same answer even though the shape and orientation of the galaxy would change.
It turns out that if v is very large, comparable to the speed of light c, Newtonian mechanics is incorrect. (You could say that Newtonian mechanics is wrong but a superb approximation for low speeds.) If you say that p=mv it turns out that momentum is not conserved for an isolated system at very large speeds. However, since momentum conservation is such a powerful way to solve problems, we redefine momentum (in the theory of special relativity), to be p=mv/√(1-(v ²/c ²)), momentum is conserved again and we still have p ≈mv for small v. It also turns out that, as a result of this new definition of p, we can write that E=√(p ² c ²+m ² c ⁴) where E is the energy of a particle of mass m. So if the particle is at rest, p=0 and E=mc ²; if the particle has no mass, p=E/c.
No more significant than if a billiard ball has momentum—it just does.

I have deleted your question about angular momentum—it is off topic.

QUESTION: I am a high school student interested in relativity and I recently read an article about relativity . The article stated that the "The combined speed of any object's motion through space and its motion through time is always precisely equal to the speed of light." For an object moving at 90% the speed of light, it should only be moving at 10% the speed of light through time. I assume that means that time should pass only at 10% the actual speed of time for the object (correct me if I am wrong). However based on the Lorenz factor, time passes at 0.43 the actual speed of time for the object. Why is this so? Furthermore when time dilation occurs it is only seen by someone else in a stationary frame of reference. In the moving object's frame of reference time does not slow down at all. Does this mean that the combined speed of the moving object's motion through space and time can be more than the speed of light in the moving object's frame of reference? Can the moving object go beyond the speed limit in its frame of reference?

ANSWER:
Look closely at the example given: "To get a fuller sense of what Einstein found, imagine that Bart has a skateboard with a maximum speed of 65 miles per hour. If he heads due north at top speed—reading, whistling, yawning, and occasionally glancing at the road—and then merges onto a highway pointing in a northeasterly direction, his speed in the northward direction will be less than 65 miles per hour. The reason is clear. Initially, all his speed was devoted to northward motion, but when he shifted direction some of that speed was diverted into eastward motion, leaving a little less for heading north." The speed in the northward direction will now be v _N=65cos45⁰=46 mph; his velocity in the eastward direction will be v _E=65sin45⁰=46 mph. His total velocity will be √( v _N ²+v _E ² )=65 mph, not ( v _N+v _E )=92 mph. In relativity N and E now are x and t for the stationary observer and x' and t' for the position and time of the moving observer as seen by the stationary observer. The catch, though, (which I presume is why the author of your article avoided these details) is that time and space are slightly different from space (N) and space (E) in that to get the length of the vector you calculate the square root of the difference of the squares instead of the sum. So the speed through spacetime would be √(c²-v² ). So, the stationary observer will see a "spacetime speed" of v _spacetime=√(c^2-v² ) and the "space time distance traveled" by the moving observer as seen by the stationary observer would be d _spacetime=v _spacetime t' where t'=t/√(1-(v ²/c ²)). If you do your algebra you will see that d _spacetime=ct indicating that the stationary observer sees the moving observer having a speed of c through spacetime.

QUESTION:
Bodies of water bend with the curvature of the planet. How large would a body of water have to be in order to measure a difference of 1 inch from one end to the other.

ANSWER:
I often get questions like this. I have used this figure many times before. Here R=6.4x10⁶ m is the radius of the earth, d=1 in=0.024 m is your 1 inch, θ is the angle which subtends the arc length, call it s, you seek. From the triangle you can write cosθ=R/(R+d)=[1+(d/R)]^-1≈1-(d/R)+… where I have done a binomial expansion of [1+(d/R)]^-1because (d/R) is extremely small. Now, because θ is also very small, I can represent cosθ by the expansion cosθ≈1-½θ ²+… so (d/R)≈½θ ². Finally we can write that θ=s/R. If you now solve for s you will find s≈554 m.

QUESTION: Hey! So, somebody is standing on Earth, and they measure the distance from Earth to some star to be D. Now, they hop in a spaceship, and travel 90% the speed of light towards the star. How will they measure the distance between Earth and the star now? <D, D, or >D? I initially thought they would measure to be <D, because I've heard of how length contraction works. After I thought about it more, I changed my guess to be D, because I thought ONLY the spaceship would experience length contraction, but I could be wrong there (I'm not 100% familiar with the phenomenon of relativistic length). Now I'm stuck between D and <D, and I'd greatly appreciate if you could clear this up!

ANSWER:
Length contraction says that a length which is moving is shortened. From the perspective of the spaceship the distance between earth and the star is a length which is moving backwards relative to the the spaceship. It is therefore <D. A meter stick on the spaceship, however, will be seen by the passengers to be 1 m in length.

QUESTION: magnetic force on charge q moving with velocity v =qV x B if i observe this charge from a car moving with same speed and direction as that of q than it velocity as observed by me will be 0 so the force will be 0.i am not able to understand this dilemma at one time force non zero and at other time it is 0

ANSWER:
The problem is that the electric and magnetic fields in one frame of reference are not the same as in another moving frame. (This is special relativity.) In your case you first start with a magnetic field and zero electric field. Suppose that the magnetic field is in the y-direction, B=jB, E =0, and the velocity of q is in the x-direction, v=iv. Then the force would be F = k qvB in the z-direction. In the moving frame the new fields would be B'=jγB and E' = kγvB, where γ=1/√(1-(v/c)²). Note that E'=v x B' ; therefore the force, as seen in the moving frame is F' =q E' =q v x B' = kγqvB, as you would expect. Note, however, that F' ≠ F , they differ by a factor of γ; this is because force is said to be not Lorentz invariant and it is not really a useful quantity in relativity.

QUESTION:
We can see things billions of light-years from Earth. This means that light photons have traveled for billions of years at the speed of light to reach us. Why don't those photons slow down or stop? Is there no energy consumed over that vast distance in order to keep that photon moving forward?

ANSWER:
It is a law of physics that photons in a vacuum can only exist moving with the speed of 3x10⁸ m/s. So, nothing has to "…keep that photon moving forward…" But, space is not really a vacuum and not 100% of photons make it over such vast distances. Some interact with the occasional molecule they might encounter and are changed or scattered. Some find themselves striking a star or planet and being removed from the stream coming from the source. Some are deflected by the strong gravity near galaxies. Some encounter a black hole and disappear altogether. Because space is so empty, though, the majority come through unchanged.

QUESTION:
The light emitted from a light bulb is thermal radiation. Probably the rushing electrons cause the atoms to vibrate and this vibration will cause photons to be emitted with a Gaussian distribution in the EM spectrum. Still i wonder. Why is the vibrating of the atoms causing EM radiation in the visible spectrum and not lets say microwave or x-ray part of the spectrum. Also, I still not sure where the photons pop into existence. Is it from all the electrons , in all shells and perhaps also the vibrating nucleus?

ANSWER:
All objects are always radiating and absorbing thermal radiation. It is electromagnetic radiation. Many objects are well-represented by black-body radiation which you might want to research a little bit. As you can see from the plot of black-body radiation at 5000 K above, all wavelengths are present, not just visible light. It may appear that there is no very short wavelength radiation, but at this temperature it is just too small to register on the graph. (Incidentally, this is not a gaussian curve.) Atoms or molecules in a solid or liquid have electric charge distributions (nuclei and the surrounding electron clouds), most importantly dipole moments, which oscillate in ways which depend on the temperature. An oscillating charge distribution looks like a tiny antenna and radiates the energy. These "antennas" are the source of the radiation. Historically, trying to understand the black-body radiation classically was what was the first indication of quantum physics. The oscillators must be quantized which means that only discrete packets of radiation are emitted—your photons.

Q&A OF THE WEEK, 2/5-2/11 2017

QUESTION:
I work in a high school where this question was posed by one of the pupils in a class I support. The question is this.... If you could attach a rope to a rocket, which would also be attached to earth, and sent it into space (out of our atmosphere) until the rope went taught and then cut the string. Would it stay in space or would it fall back to earth?

ANSWER:
This is one of those problems which I had fun with and I hope it will not be too exhaustive an answer. I will make the following assumptions:

the rocket always goes straight up;
the rocket stops moving vertically when the rope is taught;
the rope is cut the instant that the rocket stops;
fuel and the weight of the rope are not issues; and
the launch is from the equator. This makes things much simpler and I will briefly talk about a similar launch from some latitude at the end.

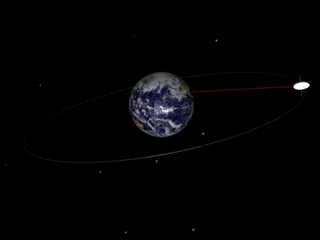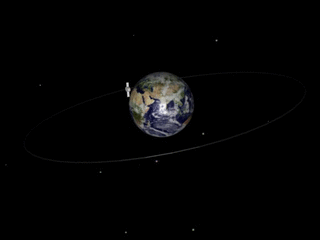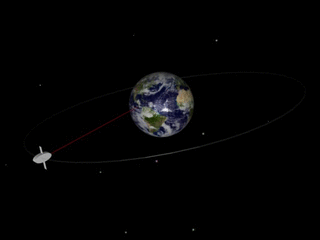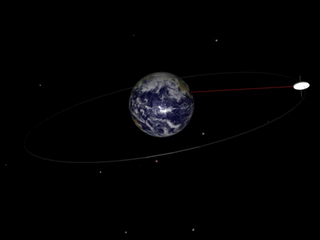My view of this problem, therefore, is the same as if the rocket were on top of a very long stick vertically straight up and the stick is suddenly removed.

The thing to appreciate is that even though the rocket goes straight up, it will have the same angular velocity ω as the earth so its speed will be ω(L+R) where L is the length of the rope and R is the radius of the earth. The angular velocity is ω=[(2π radians)/(24 hours)]x[(1 hour)/(3600 seconds)]=7.27x10^-5 s^-1. If L is just right, the rocket will assume an orbit like the geosynchronous communication satellites; this turns out to be if L=5.6R.

So, if the rope happens to be 5.6 times larger than the radius of the earth, the rocket will remain (apparently) stationary above its launch point; it is actually going in a circular orbit with a period of 24 hours. (The animation above illustrates this, although not to the correct scale.) For any other L the orbit will be an elipse with the center of the earth being at the focus. Visualize.
If L>5.6R, the starting point of the rocket will be the perigee (closest point to the earth) of its orbit. Visualize.
If L<5.6R, the starting point of the rocket will be the apogee (farthest point from the earth) of its orbit. Visualize.
For L<5.6R, though, there will be some critical distance L=L_c when the perigee of that orbit is exactly equal to R; in that case the orbit will just skim the surface of the earth. After some laborious algebra I found that L _c≈3.7R, about 2.2 earth radii inside the geosynchronous orbit. Visualize.
For L<L_c , the rocket will crash back into the earth but not where it was launched from because it is a projectile which has a horizontal speed greater than that of the earth's surface. Visualize.
Finally, if the horizontal speed of the rocket ω(L+R) is greater than or equal the escape v _e=√[2MG/(R+L)], where M is the mass of the earth, the rocket will escape the earth and never come back. I calculated this to be when L=7.6R, two earth radii beyond the geosynchronous orbit. Visualize.

For any other latitude θ the speed of the satellite will be ω(L+R)sinθ. The resulting orbits, while all elliptical, are much more difficult to visualize and maybe we should save that for another day! However, the simplest launch of all would be from the north or south pole (θ=0⁰ or 180⁰) because it acquires no horizontal velocity (ω(L+R)sinθ=0) where the rocket would fall straight back down regardless of how high it went.

QUESTION:
Assume there are 2 black bodies, 1 with a mass double of the other. If both black bodies reach a temperature of 5000K, do both emit blue light as black body radiation, with the heavier body emitting a brighter light. Or does the heavier body emit white light while the lighter body emits blue light? Why?

ANSWER:
A black body does not radiate one color but rather a spectrum of colors. The spectrum for 5000 K is shown above. The most intense color of this spectrum is at 580 nm which is the green color shown to the right. The intensity of the light emitted does not depend on the mass, it depends on the surface area of the black body; if you double surface area, you double the amount of energy being radiated.

QUESTION:
What force causes your hands to warm up when you rub then together?

ANSWER:
Friction. But the energy to warm your hands comes from you. When you rub your hands together you are exerting a force so you are doing work. But the energy derived from your work does not speed up your hands, rather it is lost to friction and shows up as heat.

QUESTION:
I'm a science geek and an IT person who just found out that there are sixteen types of water ice. I've been googling the phenomena, and can only find discussions of the physical make-up at the atomic level. Can you help me with some discussion of the various forms of ice at a macro level? Like, what does it look like, how does it act, etc. Everything I've found is in science speak, which I really can't envision myself.

ANSWER:
Refer to the figure above which came from the Wikepedia article on ice. You can get a clearer picture there. The thing to notice is that all the ices except for ice I and ice XI occur at extremely high pressures—1000 atmospheres or higher. So, you cannot really "look" at them and say what they look like since they are formed in a containment vessel of some sort. Ice XI occurs at atmospheric pressure but only at very low temperatures. If you look at the Phases section of the article, you will find links to separate articles for all 16 forms of ice where you can get information about their properties. Although the terminology for the crystal structure is pretty "science speak" as you say, you will find usually pretty comprehensible pictures of these crystal structures. I think you would find these articles about as understandable as you will find.

QUESTION:
If a good absorber is a good emmiter also then why don't we prefer to wear black clothes in summer or in hot conditions?

ANSWER:
Because we are better off if we do not absorb any heat in the first place. We wear a poor absorber.

QUESTION:
Can electric field and magnetic field collide to each other? If yes what will happen when they collide to each other.

ANSWER:
Two fields "colliding" really does not have any meaning. Certainly an electric field and a magnetic field can exist at the same time and location. If either is changing at that time, it will cause the other to change.

QUESTION:
How much physical energy is exerted in a "typical" gym and how does that compare to the amount of energy necessary to operate that same facility. I am wondering if there have been any investigations into redirecting this type of activity towards more productive ends.

ANSWER:
A person doing vigorous exercize may expend about 10 kCal/hr≈2.8 W. The gym would probably consume a few kilowatts so you would probably need a couple of thousand folks to generate that much power. I don't think you are on to something here!

QUESTION:
If vision works when we receive the reflected wavelength of white light from a particular object. Also we knew angle of reflection depends upon incidence angle, how so many people could possibly see the same object unless they stood in the path of reflected wavelength.

ANSWER:
Because the surface is not smooth like a mirror, the angle of reflection is not equal to the angle of incidence.

QUESTION:
Why is it easy to accelerate tiny sub-atomic particles like electrons close to the speed of light compared to large macroscopic objects like spaceships?

ANSWER:
There are lots of ways you could explain this. For example, Newton's second law states that a=F/m where a is the acceleration of an object of mass m when acted on by a force F. Suppose you exert a 1 N force on an electron (m ≈10^-30 kg) and a space ship (m ≈10⁶ kg). Then the acceleration of the electron (initially) is 10³⁰ m/s² and that of the space ship is 10^-6 m/s².

QUESTION:
If atoms at room temperature move around at roughly the speed of a jet airplane, how fast do atoms that make up a jet airplane move when said airplane is moving (at room temperature)?

ANSWER:
I assume you are talking about molecules in a gas. It is much more complicated to talk about molecular speeds in solids. So let's talk about the air in the airplane cabin. The speeds are distributed from very low to very high, but the most probable speed would be around 1000 mph, about twice the speed of a commercial jet. But, that does not mean that the most probable speed of molecules in a jet flying by would be around 1500 mph because the molecules measured inside the airplane would be moving in all directions so the result of adding 500 mph to all the molecules going 1000 mph would yield anything from 500 mph to 1500 mph. Measured inside the airplane, the average velocity of all the molecules would be zero because for every molecule going in one direction with some speed v there is always another going in the opposite direction with speed v. The average velocity of the air in the airplane as measured by an observer on the ground would be 500 mph. It could be thought of as like a wind in which there is a net flow of air in the direction the wind is blowing.

QUESTION:
Hi, my question relates to time dilation and the twin paradox/moving clock theory. A worked example of time dilation with a moving clock (one clock taking a relative tonitself 1 hour round trip at near the speed of light and one clock staying as a reference) shows it seemingly loosing time due to time dilation. Wouldn't this only seem to be correct until the observation of the moving clock ended? For example, the observation point which watched the moving clock is getting its informatiom from the trail of light from the journey, which shows slower time due to the speed at which it is travelling (as light is effectively taking longer to reach the observation point). However, when the travelling clock lands back on earth after an hour (relative to itself) and you were to end the observation of its journey and simply look at its landing spot, it should be there. Not only that but it should be showing the same time as the reference clock. So an hour long trip at the speed of light would only seem to take longer if you only seen it through your observation of its journey. Which would make any worked examples true up until observation ended. If this would in fact be true, wouldnt it be a more suitable explanation that our time is relative to light and that time dilation is no more than a light-trick as we only see what we see when light reaches us? Or that our time is only relative to the centre of our universe?

ANSWER:
I think you can clear up your confusion by reading the faqs for the twin paradox and for how fast clocks appear to run.

QUESTION:
I am trying to understand how to predict stopping distances at other speeds if I know a stopping distance at one speed. Let's say a car going 25 mph with studded tires on packed powder stops in 20 meters. (I got that from a study on various types of tires on various surfaces- it's realistic). What would be a good approach to finding the the stopping distance of the same car with the same tires on the same surface, if it is going 20 mph? We do not know the mass of the car, but perhaps it is accurate to create an acceleration constant that will apply for other speeds?
a=v/t and v=d/t
so therefore by combining these we get
a=v^2/d
25mph is 11.176 m/s deceleration constant:
a = (11.176m/s)^2 / 20m = 6.245 m/s^2
then can we apply the deceleration constant to the other question? What will be the stopping distance at 20 mph? 20mph = 8.94 m/s; stopping distance is 12.8m Is this valid? My applications include predicting future stopping distances at other speeds if one has experienced a stopping distance at a particular speed, and also, finding a reasonable speed for a traffic situation near where I live, where there is limited visibility.

ANSWER:
Your final answer of 12.8 m is right, but your method is wrong. Your answer for the acceleration (and stopping time if you had calculated it) is wrong. Your principle error was that d/t is the average velocity, not the starting velocity; the velocity is changing the whole time. In this case, uniform acceleration, the average velocity is ½v ₀so your acceleration is wrong by a factor of 2; a=-3.12 m/s². The correct expression for the stopping distance is d=½v ₀ ²/a where v ₀ is the initial velocity and a is the magnitude of the acceleration. The force which stops the car depends only on the nature of the rubbing surfaces and the weight of the car. But the weight of the car cancels out when you calculate the acceleration, so the acceleration is independent of both the weight and the initial speed. Therefore your guess that you can use one datum to determine the acceleration and then use that for all other speeds is correct; the added bonus is that it is also independent of how heavy the car is as long as it is the same road surface with the same tires.

QUESTION:
An interesting question came up amongst my friends and me resulting in differences of opinion that I hope you can settle. Question: If an object is dropped from a fixed position while travelling in a moving jetliner(say 300+ MPH) would the same object dropped from the same position while not moving land on precisely the same spot? ie not a micron different. Of course all variables being equal.

ANSWER:
Absolutely they would not land in the same place. The way you describe it is a little confusing: "dropped from a fixed position while travelling" is kind of ambiguous isn't it? I assume that it is like dropping a bomb from a plane; the plane and bomb are both moving forward. Neglecting air drag, the bomb will land directly under the plane if the plane continues moving with constant speed in a straight line. The object dropped from rest exactly where the plane was when it dropped the bomb will land directly below the drop point. If air drag is taken into account, the bomb will land somewhat behind where the plane is. See an earlier answer.

FOLLOWUP QUESTION:
The scenario involves an object dropped from a fixed point inside a moving airliner and hitting a point under it but still inside the aircraft. No bomb dropping. Then a repeat of this operation while the airliner is sitting still. Does it hit the same spot in each case?

ANSWER:
Sorry, I misunderstood. In an elementary physics class, it is assumed that the only force which acts on the object is its own weight, a force toward the center of the earth. And actually that is true. However, it is also assumed (although not always stated) that the plane is moving in a straight line with constant speed; that is not true because if the plane maintains a constant altitude it is actually moving in a circular path above a spherical earth and the earth itself is spinning on its axis. If the observer is in the airplane (which she is), Newton's laws are not true because in either case the experiment is being done in an accelerating frame. However, there is a neat trick to make Newton's laws work in an accelerating frame by introducing fictitious forces; the best known fictitious force is the centrifugal force. The force (real+fictitious) which acts on the falling object depend on the direction the plane is flying, its speed, and its latitude. These are different for your two experiments and therefore the two objects would not land precisely at the same spot. To read more detail on these fictitious forces, see an earlier answer.

Finally, there are two places on earth where the fictitious forces are zero and therefore the two objects will move identically—at the north and south poles.

QUESTION:
An object travels at a very high speed relative to some planet. Its velocity is normal to the gravitational field lines of the planet at a particular instant. At that instant, does the gravitational attraction between the two bodies increase due to the object's relative motion or does it stay the same as if the object was not moving at all?

ANSWER:
The object moving at high speed has an increased mass and therefore feels an increased gravitational force.

QUESTION:
What causes the curvature of spacetime/gravity to be so strong around black holes? Is it due to their density (mass density/energy density)? If not what is it due to? And why dont other extremely dense stars like the sun exhibit properties like black holes

ANSWER:
For any spherically symmetric mass distribution the gravitational field is proportional to the mass m and inversely proportional to the square of the distance from the center 1/r ². Because a black hole is a singularity (zero size) it is possible to get very close to the center where the field will be huge. Also, many black holes are very much more massive than a typical star. A regular star might have a very big mass, but it is spread out over a very large volume; inside the star itself the field decreases linearly to zero at the center.

QUESTION:
If you were able to drive your car with forward acceleration in outer space and you rolled the window down and stuck out your arm, would it be pushed back like it would here on earth? This isn't a homework or test question, it is a question that came up in a fun discussion at work the other day...

ANSWER:
You had better have your space suit on because outside the car there is no air in outer space. And the fact is that the main thing which causes your arm to be pushed back here on earth, particularly for high speeds, is the air drag, the apparent wind you perceive to be blowing from in front of you. That is totally absent in space. However, you have specified that the car is accelerating. When you accelerate forward, it feels as if there is a force pushing you (and your extended arm) backward. There is no such force (which is why we call it a fictitious force), but it feels like it because your accelerating arm needs a forward force (your shoulder provides it) to accelerate it and your brain interprets this as there is something pushing your arm backward which your shoulder counters. Here on earth, unless your acceleration is very large and/or your speed is very small, this force is pretty small compared to the air drag. So the answer to your question is that your arm will be pushed back but not "…like it would here on earth…"

QUESTION:
I was wondering what would happen if an object, say a cube, were travelling toward you at a relativistically interesting speed. Its motion is strictly in the x component in an XYZ coordinate plane. Would you see a length contraction in the dimensions of the cube in all three dimensions or just the x component? Also I was curious about the effects of the length contraction on the observed density of the cube. Observed mass goes up as velocity does, and you observe a length contraction in one or more dimensions (depending on previous answer). Therefore the density would go way up. Is this a proper interpretation of relativity?

ANSWER:
As I have said before, saying that mass increases with speed is a matter of taste. It turns out that in special relativity the linear momentum p is not conserved if momentum is defined as p=m ₀ v where m ₀ is the inertial mass at rest. If you redefine p to be p=m ₀ v/√(1-(v ²/c ²)), momentum of an isolated system is constant. You can interpret this as simply a redefinition of p or that the mass has increased so that m= m ₀/√(1-(v ²/c ²)). That said, let's answer your question assuming that mass increases.

Length contraction occurs only along the direction of motion. Since mass increases by a factor 1/√(1-(v ²/c ²))) and volume decreases by a factor of 1/√(1-(v ²/c ²)), density increases by a factor 1/(1-(v ²/c ²)).

QUESTION:
if a cat fell from 100 feet how fast was the cat in mph falling when it hit the ground

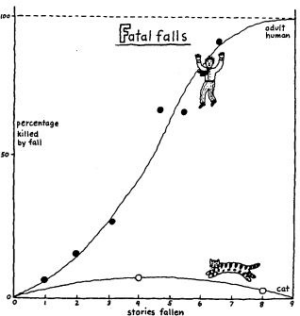
ANSWER:
The terminal velocity of a cat is about 60 mph and that speed is achieved after falling about 50 ft. Therefore falling from 100 ft the speed would be about 60 mph. See earlier answers (1 and 2) for more details. Keep in mind that all cats are not the same size, weight, or fuzziness, so this can only be an approximate answer. It is interesting that about 10% of cats falling from 5 stories are killed but fewer from higher stories because, once reaching terminal velocity, they can relax, spread out (to slow down) and get ready to hit.

QUESTION:
E=MC^2. It implies that energy and mass are exchangeable and consistently so. My problem comes with c^2. How is this possible? c= the speed of light, if I am not mistaken and one of the fundamental laws of the universe is its speed limit, that of c. So how is c^2 possible?

ANSWER:
Consider the following: you have a few hundred square tiles, and they have varying sizes. I will use d to specify the length of the side on any particular tile. However, due to some fundamental law of the universe, none of these tiles is allowed to have to have d>d _max=4 cm. Now suppose that I write an equation for the area of any of these tiles, A=d ². Now one of these tiles has a size of d=3 cm (not violating our fundamental law) and so its area is A=9 cm². But wait, how can that be? Since d ² is more than twice as large as d _max, this must violate our fundamental law of the universe, right? Of course not. The area of a square is simply a different thing from the length of the side of a square and does not even have the same units (cm vs. cm²).

QUESTION:
I am a weight lifter and want to calculate how much "work" I do when performing the deadlift. I did the math and want to ensure my concepts and calculations are correct, as it has been a while since I took physics. Here is what I did: I am lifting 225lb (1000.85 newton) a distance of 0.613m. So the work (in joules) = 1000.85n X 0.613m = 613 joules. I did 32 repetitions of this in total, so the total work would be 19,632.64 joules. So, if I convert that to watt hours, it is about 5.45 watt hours. Does this mean that to do that same amount of work, 5 watts for 1 hour would be required? Or 20 watts for 15 minutes? Or 300 watts for 1 minute? Did I use the right calculations? Ultimately I want to compare several of my lifts to see how much total work I performed (for example 10 sets of 5 reps on Bench Press at 150lbs VS 6 sets of 7 reps on Deadlift at 225 lbs)...

ANSWER:
All your calculations are correct (allowing rough rounding in "__ watts for __"). The problem is that simple physics like this is not really a good approximation to how biological systems are actually working. If you simply hold a weight with a horizontal arm, physics says no work is being done, but you and I know that sugar is being burnt to provide energy to hold the weight there. Likewise, physics says you are doing negative work when you lower the weight (cancelling out the positive work you did lifting it) but I suspect this lowering also requires you to actually use energy, that is do positive work. The explanation of how work is being done is given in an earlier answer.

QUESTION:
This is quite for a long time that I'm thinking about a question in Galilean kinematics which brings me to a paradox, which I cannot solve myself. Consider a body with a mass m and velocity V ₁ in one reference system and V ₁ + V' in another one. Now let's say this body starts slow down and its velocity change is ΔV in both systems. Simple algebra shows that the kinetic energy change in the 1st system will be ΔE ₁ = mΔV/2(2V ₁+ΔV) and in the 2nd system ΔE ₂ = (mΔV/2)(2V ₁+ΔV+2V') i.e. its different in different reference systems. Now if we imagine that this slow down and kinetic energy change was due to the friction it follows that the amount of heat released is different for different reference systems! Nonsence! It should be a mistake somewhere.

ANSWER:
The first thing to appreciate is that energy is not invariant under Galilean transformation. This is easy to appreciate since a mass with speed v has kinetic energy K=½mv ² but zero kinetic energy in a frame moving with it. Therefore, the change in kinetic energy will be different in different frames. However, the work-energy theorem (ΔK=W where W is work done by external forces) will be true in all frames, just not the same numbers in all frames.

In the first frame in your example, where m has speed v ₁, the floor is, I assume, at rest. To make the algebra simpler and the explanation easier to grasp, I am going to let m come to a complete stop, Δv=-v ₁. Then, when m moves some distance s and the frictional force is f, the work done is W=-fs and so ΔK=-½mv ₁ ²=-fs. You can deduce that the heat generated is ½mv ₁ ²; all other frames will see this amount of heat. Now, in a frame with speed v' moving in the same direction as v, you can easily show that ΔK'=-½mv ₁ ²+mvv'. You already know that -½mv ₁ ² is the heat and mvv' is simply the amount that ΔK is different in this frame. If you calculate the work done in this frame, it is different because the distance m slides is different; but, if you do that you will find, as expected that
W=-½mv ₁ ²+mvv'.

One more special case. Suppose v'=½v. You should be able to convince yourself that m originally is catching up with the moving frame but then stops and turns around and ends up where it started from; thereafter it moves with constant speed v'. The total distance it has traveled in the moving frame is zero and so W=0 and therefore ΔK'=0. So the heat is not anywhere evident here even though you would feel it. In this case you would find W=-½mv ₁ ²+½mv ₁ ². Now you can see where that heat is hiding, right?

So, if you want to most conveniently determine the amount of heat generated, you apply the work-energy theorem in the frame where the surface is at rest. This is because to the moving observer the surface is moving as well as m. The moving observer has to correct for that motion by calculating m's motion relative to the surface. m's motion relative to the second observer is not really relevant in calculating the heat generated.

Thanks to R. M. Wood and A. K. Edwards for helpful comments.

QUESTION:
I'm trying to come up with an equation at work on how to figure out how much a parent roll of toilet paper weighs just by measuring the distance from the core to the outside of the roll without taking it out of the machine. For instance 1inch of paper on the out of the roll will not weigh the same as 1 inch of paper from the core. The measurements I know are the weight of the parent roll when we start using it, the core diameter, core weight, and distance from the edge of the core to the outside edge of the roll before it's started. As it is running we can measure the current distance from the core edge to the outside of the roll while it is running. My question is how do I calculate a equation to determine the weight of the roll at any given time based on the distance from the edge of the core?

ANSWER:
Not really physics, but I can do it. Notation:

W ₁ is the weight of the parent,
W ₂ is the weight of the core,
W ₃=W ₁-W ₂ is the weight of the paper in the parent,
R ₁ is the radius of the parent,
R ₂ is the radius of the core,
L is the length of the roll,
V ₁= πL(R ₁ ²-R ₂ ²) is the volume of the paper on the parent,
W is the weight of the paper on the partially used roll,
R is the radius of the partially used roll, and
V=πL(R ²-R ₂ ²) is the volume of the paper on the partially used roll.

You may be interested only in the final answer, but I will outline the solution for anyone interested.

The density of the paper is ρ=W ₃/V ₁=W/V.
Therefore, W=W ₃(V/V ₁)=W ₃ (R ²-R ₂ ²)/(R ₁ ²-R ₂ ²).
What you want, is the weight of the whole partially used roll, W+W ₂=W ₂+W ₃(R ²-R ₂ ²)/(R ₁ ²-R ₂ ²).

So, just plug in your measured values and you will have the weight of the partially used roll. Incidentally, you say "distance from the edge of the core". If this (call it D) is more conveniently measured you can replace R in the equation above by (D+R ₂) which results in
W+W ₂=W ₂+W ₃(D ²+2DR ₂)/(R ₁ ²-R ₂ ²).

QUESTION:
I'm a writer. I'm working on a story. It's sold actually, but they want some changes and I'm trying to figure out the science..

IDEA: A distant planet picks up broadcasts from Earth, so the inhabitants have some knowledge of us, and know that life is out there. A "man" on the alien planet gets part of his consciousness encoded into a light beam that is sent out into space. When it hits earth -It is able to project itself and appear to be human. When the light fades the man vanishes, leaving a message that he is long dead. (It's a love story.) But the question is what broadcasts would he have received time wise. His knowledge of earth would be limited, ending at a certain time...

This is the end/explanation. Thank you in advance for your help!

"My people developed a holographic beam so powerful it could be projected through space. Through light-years. It is more advanced than anything on Earth, so advanced that some actual particles of my being were intertwined with the particles of light being projected. So it was like I was actually here, next to you, talking to you, laughing with you. But I was not. I am not. "When we sent the beam of light traveling into space my particles were woven into it, not all of them, of course. But enough particles of my consciousness were intertwined with the particles of light so that I could interact with anyone I discovered. ...So that I could learn more about the world we'd previously only known through television broadcasts. .. "I traveled in a spaceship made of light. Now that the light has died so have the particles of my consciousness that were interwoven with the beam.... The real 'me, ' the corporeal 'me,' died HOW MANY? light years ago." Long ago, men went to sea. And women waited for them, peering out into black waters, searching for a tiny speck of light on the horizon. Now I too wait, looking out into the vast blackness of space, searching for my love, my heart, HOW MANY? light-years dead.

ANSWER:
For starters, a light year is a measure of distance, not time, so you want to say 'years' not 'light years' in your concluding sentences. (A light year is the distance light will travel in one year.) It would be better, I think, if the traveler could have learned about earth from radio broadcasts as well as television because that could take us back about 100 years ago compared with only about 50 for tv alone. His consciousness travels here at the speed of light, so he could not have come here from a distance of greater than 100 light years away from earth which is a pretty small region of the universe. (The diameter of our galaxy, the Milky Way, is about 100,000 light years.) So, the most extreme case would be that it takes 100 years for the signals to first reach his planet, then it takes his consciousness another 100 years to get here; so when his 'consciousness' arrives on earth, the stay-at-home him would be at most 100 years older and he arrives on earth 200 years after the first radio signals he received were sent.

One other detail which probably isn't that important would be you could not really carry 'particles' of consciousness (whatever that might be!) on a light beam if they had any mass at all. Nevertheless you could envision the information regarding his 'consciousness' could be carried by light.

ADDED THOUGHTS:
I did not answer one of your questions. How much information he had would simply depend on how long he waited after first receiving signals. Since the light beam would not be able to receive and interpret later signals, he would have no further information. However, if you were to put his 'consciousness particles' aboard a spaceship going 99.999% of the speed of light, all the broadcasts could be intercepted and interpreted en route and incorporated into his consciousness somehow; other timing would be pretty much the same. Or, if you simply put him on that spaceship, he would age only about half a year during the trip which the earth would see as 99.999 years. But then you would not have your dramatic sad ending!

QUESTION:
I've been given a query by a friend, and I'm having trouble finding answers! Consider the following: The tallest building in the world is 250m tall (completely fabricated stat). At the top of this building is a light detector and a clock. At the bottom of the building is a laser and identical clock. At t = 0 the laser fires a single beam of light at the light detector atop the building. Exactly 5 seconds later the laser fires another beam of light at the light detector atop the building. Therefore, at the bottom of the building 5 seconds has passed in between laser shots. How much time has passed between the light detector detecting the first and second laser beams at the top of the tower? The same, more or less? I've ben given a query by a friend, and I'm having trouble finding answers! Consider the following: The tallest building in the world is 250m tall (completely fabricated stat). At the top of this building is a light detector and a clock. At the bottom of the building is a laser and identical clock. At t = 0 the laser fires a single beam of light at the light detector atop the building. Exactly 5 seconds later the laser fires another beam of light at the light detector atop the building. Therefore, at the bottom of the building 5 seconds has passed in between laser shots. How much time has passed between the light detector detecting the first and second laser beams at the top of the tower? The same, more or less?

ANSWER:
Since you acknowledge that the height of the building is immaterial, let me make it 1.0 light seconds tall. (A light second is the distance light will travel in one second.) So the first pulse is observed at t=1 s and the second at t=6 s, an elapsed time of 5 s.

FOLLOWUP QUESTION:
the identical clock statement simply means that if they were switched around and the experiment performed again, the result would be the same. The answer lies in general relativity.

ANSWER:
OK, I did not realize you wanted to get so exacting! I am still going to use a building 1 ls=3x10⁸ m high to keep the numbers from becoming impossibly small. Indeed, general relativity tells us that the stronger a gravitational field is, the more slowly a clock will run. This is called gravitational time dilation (and is directly related to gravitational red shift). The rate at which a clock runs slower in a gravitational field (MG/r ²) is √[1-(2MG/r)] where M is the mass of the source (the earth in your case), G=6.67x10^-11 N⋅m²/kg² is the universal gravitation constant, and r is the distance from the center of the source. If some time t elapses on a clock in zero gravitational field, the time which will elapse for other clocks is t/√[1-(2MG/r)]. For our purposes I will assume that the zero-field clock will measure 1 s for a pulse traversing your building.

After doing some arithmetic I find that if t elapses on the zero-field clock, t'=t[1-(4.4x10^-3/r)] elapses on another clock. So, for the first pulse where both clocks have begun at t'=0, the elapsed time of the two clocks will be t' _bottom=(1-6.9x10^-10) s and t' _top=(1-1.5x10^-11) s. The upper clock will will measure a shorter time by about 6.8x10^-10 s=68 ns.
Now, we need to specify who determines when 5 s have elapsed. The most sensible choice would be the guy at the bottom of the building who will be triggering the laser. When his time is t' _bottom=5 s, the zero-field time is t=5/(1-6.9x10^-10)≈(5+3.5x10^-9) s and (this is tricky) the top clock will measure t' _top=(5+3.5x10^-9-6.8x10^-10x5)=(5-1.0x10^-10)s.
We know from the first pulse the additional time on both clocks, so we can now calculate what each clock reads when the second pulse hits: t' _bottom=(5+1-6.9x10^-10)=(6-6.9x10^-10) s and t' _top=(5-1.0x10^-10+1-1.5x10^-11)=(6-1.2x10^-10) s.

The top clock will see 57 ns more time elapse than the bottom clock. I believe that if you use the 250 m tall building, things would simply scale and time differences would be 250/3x10⁸=8.3x10^-7 times smaller.

QUESTION:
Now, I know the centre of gravity can change depending on how close to uniform the gravitational field is, and it is where the weight appears to act from. But, what is the centre of mass? Ok, it is a constant; doesn't change; and in an uniform gravitational field the two centres overlap; but how do you define the centre of mass without referencing centre of gravity? An online source said it is the point from which the mass is 'equally distributed in all directions' for an object; but I can have irregular shapes. What does that source means? Or is the centre of mass defined in another way? I am really confused!

ANSWER:
Actually, the center of mass is the fundamental quantity, not center of gravity. The the position r _cm of the center of mass for a collection of point masses is defined as r _cm=[Σm _i r _i]/Σm _i where r _i is the position of the point mass m _i. If you have a continuous mass distribution with mass density ρ( r ) you have to integrate over the whole volume to get r _cm: r _cm=[∫ rρ( r )d r ]/∫ρ( r )d r . Notice that in both cases the denominator is just the total mass.

QUESTION:
When I was very young, I used a hand-held fish scale to try and measure my own weight by attaching the hook (normally placed in the gills of the fish just caught) to my belt and then pulled up on it. I'm interested in the physics behind my folly and, expanding it further, if the scale was attached to a light (not heavy) bar (that would support more than my weight) and the scale could measure a fish weighing more than me, and I was strong enough to lift more than my weight above my head, how close could I expect to get to seeing my weight on the scale (attached to the bar I'm pushing up, and a belt-device around my waist)?

ANSWER:
The way you always solve a statics problem like this is to first choose a body, then apply Newton's first law which states that the sum of all forces on the body must equal zero; I choose the scale as the body. What are the forces on the scale itself? Your hand pulls up with a force F _hand, your belt pulls down with a force F _belt, and the earth pulls down on the scale (its weight) with a force W _scale. These three have to add to zero which means that F _hand=F _belt + W _scale. Now, the scale is calibrated so that it reads zero when F _belt =0, so the scale will read whatever force your hand exerts up. Note that when you do this analysis, the desired quantity, your weight, never appears; everything would be just the same if you weighed 1000 lb. Regarding your second question, it is really no different from the first question: simply replace 'belt' by 'bar' everywhere. In either case you would observe the scale reading your weight when you pulled up with a force equal to your own weight.

FOLLOWUP QUESTION:
Thank you! So it sounds like it wasn't a folly after all (except for the fact that the scale I used wouldn't support my weight at that age).

ANSWER:
Of course it was folly, total folly! Doing this experiment gives you absolutely no information about your weight. Only if you already knew your weight and were able to pull with a force that hard would the scale read your weight.

QUESTION:
I'm having a discussion on a website that came up because of another post. That post asked the question (paraphrased) If you connected a wire to your mouth and another (unstated) orifice, how fast would you have to travel around the earth to create enough current to electrocute yourself? One of the other posters wanted to know if the voltage would be the same "going" through your body as through the wire. And wouldn't your body have current induced also? The answer for the induced current in the wire I can deal with, But haven't enough electro/biology (I just made that up) to explain why ones body wouldn't have current induced in it. I know intuitivly why but can't explain it satisfactorily to him. Can you help me out here (in colloquial English)? I'd appreciate it if you can and willl

ANSWER:
The body is certainly not a perfect insulator or else you would never have to worry about getting electrocuted. The physiology is very complex and variable, and it doesn't seem you want to get into too much detail either, so I will just talk qualitatively. Two important features:

A voltage large enough to drive a large enough current through your heart will kill you.
A conductor moving through a magnetic field will have a voltage induced across its ends. (Details depend on direction of the field and the direction of the velocity of the conductor. Just assume that you have a straight wire moving perpendicular to the field.)

So the wire will have a voltage across its ends and will therefore look like a battery. Similarly, the body will have a voltage of the same polarity (say positive at the mouth and positive at the end of the wire in your mouth) but with a much smaller voltage than the wire; this would create a circuit looking like two batteries, one weak and one strong, which would drive a current through the weaker battery (your body). So, the idea works if you move fast enough. But, the earth's magnetic field is really weak and the speeds would be impossible to achieve without burning everything up in the atmosphere I would bet. Let's just do a rough calculation. The voltage V is about V=BLv where B is the field, L is the length, and v is the velocity. I will take L=1 m, v=18,000 mph≈8000 m/s (low earth orbital speed), and B≈5x10^-5 T. So the voltage would be less than half a volt! Have I been colloquial enough for you?

QUESTION:
Would it be possible physically to encapsulate a black hole with solar panel type devices and use its energy to power a civilization? Like when we reach trans-galactic civilization status and run across a black hole and we want to utilize it.

ANSWER:
Well, that is a pretty crazy idea because a black hole is an energy sink, not an energy source!

QUESTION:
im struggling to get a grasp of this. say car A and car B are travelling at a constant speed, maintaining same distance in between. form car A you shoot a gun 90 degrees up. which vehicle is the bullet likely to fall in. is car A or B?

ANSWER:
Before you fire the gun, the bullet in it is already traveling along with you in car a with the same speed as the car. When you fire it up it goes up with some speed but it continues moving parallel to the ground with car A also. Since there are no forces in the horizontal direction acting on it (neglecting air drag), it will go straight up and straight back down as seen by car A. Someone on the ground will see it go in a parabolic path beginning and ending in car A.

QUESTION:
I don't quite understand escape velocity. I know rockets have to reach 7mi/sec to leave earth's gravity but If I set off in my hypothetical spaceship and I moved at a constant 7 miles per minute on a trajectory perfectly perpendicular to the earth and directly above its launch pad (until I hit a geosynchronous orbit). If I can maintain this velocity away from and perpendicular to the earth what could possibly be stopping me from escaping its gravity?

ANSWER:
The escape velocity is defined as the speed an object must have at the surface of the earth (neglecting air drag) to escape. Obviously, as you note, if you could could continue pushing on something to keep it moving a speed of 1 cm/s, it would eventually get as far away as you liked. For more on escape velocity, see the FAQ page.

QUESTION:
I was wondering if the charge of a particle increases as its mass does (at relativistic velocities). For example, if a quark is going very fast, does its charge increase the same proportion as its increase in mass?

ANSWER:
No, electric charge is strictly conserved.

QUESTION:
When a photon loses energy (Redshifts) climbing up thru a gravitational field, does the photons decreased energy go into the mass of the gravitational field itself? According to GR, the gravitational field itself contributes to the mass of the system. For earth, it is very small. When I elevate a massive object in a gravitational field, I can say the "potential energy" is in a very small increase of the mass of the object. But photons have no mass! And are never at rest! The only thing I can think of is that the photon "transfers" energy to the gravitational field itself, which appears as a small increase in mass of the field.

ANSWER:
Let's think of a star emitting a photon of frequency f. Initially an energy of hf is removed from the star. But, by the time that the photon is very far away the star, it has lost some amount of energy Δhf, so the net loss to the star and its field is hf-Δhf. At the instant the photon is created, the mass of the star is reduced by hf/c ². But when the photon, which is losing its energy to the field, is far away, the energy of the field will have increased by Δhf/c ²; I would not use the terminology "mass of the field" since the field has energy density, not mass. But now, it seems to me (not a cosmology/general relativity expert) that there is a bit of a paradox: we always associate a given mass with a particular gravitational field, so the field should have the energy content associated with a mass M'=M-hf/c ². But, in fact, the field would have energy content associated with a mass M'=M-hf/c ² +Δhf/c ². I am guessing that the field and the mass somehow "equilibrate" so that the final mass of the star is consistent with the energy of the final field. (I could easily be wrong! Perhaps it is only meaningful to look at the total energy of the star and its field. Whatever the case, I would not talk about mass of the field.)

QUESTION:
Considering a lack of strong ambient light sources, such as the sun, is the exterior glass of a spacecraft, the part that comes into contact with the vacuum of space, cold, neutral, or hot? Would it depend on the temperature inside the craft itself, or would the vacuum have enough of an impact on it to change it?

ANSWER:
It is just the same as a window in your house in winter. The inside surface will be in equilibrium with the air in the room and the outside surface will be in equilibrium with the air outside. Then heat will be conducted from inside to outside at a rate proportional to the temperature difference. If the sun is shining directly on the window, absorption of the radiation would raise the temperature of the outside surface somewhat.

QUESTION:
Why isn't Hawking radiation trapped in a black hole's gravitational pull and eventually sucked right back into the black hole?

ANSWER:
What happens is that pair production occurs near the Schwartzschild radius. One particle of the pair is outside that radius and can therefore escape.

QUESTION:
"IF" we violate the laws of conservation, what would happen?

ANSWER:
There are so many such laws that no single answer could cover it all.

FOLLOWUP QUESTION:
But is it possible to violate the laws even tho we don't know how since its just a law and some laws are meant to be violated...sorry for my curiosity, I just some opinions from a Physicist

ANSWER:
I would say that if a "law" is properly stated, it is not "meant to be violated". Again, there are far too many conservation laws to discuss. But let me give you just a couple of examples of how a law can be misstated but, if properly stated, it cannot be broken.

Energy conservation:
1. Incorrect: the total energy of any system is conserved. In fact you can change the energy of a system by doing work on it.
2. Correct statement: the total energy of any system is conserved if no external forces do work on it.
Electric charge conservation:
1. Incorrect: The total electric charge of a system must remain constant. In fact, you can always add or subtract charge from a system.
2. Correct statement: The total electric charge of an isolated system must remain constant.

These laws are laws because they are always found to be true and it is rather pointless to ask "what if". If energy conservation were not true, then energy could suddenly appear out of nothing.

Only if there is some overriding physical law could another be broken, but only within certain constraints. For example, the Heisenberg uncertainty principle says that it is impossible to precisely know the energy of a system for a short enough time, ΔEΔt~10^-34 J⋅s where ΔE is the amount by which you change the energy of a system and Δt is the time during which the energy is changed by that amount. For example, 10^-20 J could appear out of nothing for as long as 10^-14 s; after the time had elapsed, though, it would have to disappear again.

QUESTION:
Are there any similarities between light waves and sound waves? For example, When I pluck a guitar string while placing the guitar parallel to the tv, I can see waves that I previously couldn't see under visible light. The color blue seems to work best.

ANSWER:
The picture on your TV flickers at a rate of 60 Hz (times per second). Therefore it is like a strobe light. If the string is vibrating with a frequency of near 60, 120, 180,…it will appear to be frozen; sound has frequencies around these frequencies. So, you are probably seeing this strobe effect. The frequencies of light are enormously larger, hundreds of THz (10¹² Hz).

QUESTION:
What was the first thing Einstein did for the Mathematics of General Relativity? I just mean to say how did he start General Theory of Relativity?

ANSWER:
There is a story about how Einstein got the idea for general relativity, possibly not true. He was sitting at his desk in the Swiss patent office watching a workman across the square on a ladder painting a building. The workman fell off the ladder and Einstein thought to himself, "There is no experiment he can do which could distinguish whether he is in free fall in a gravitational field or is at rest in empty space." This is a statement of the equivalence principle which, along with principle of relativity (the laws of physics must be the same in all reference frames) form the basis of general relativity.

QUESTION:
If i am walking around the earth. Gravity keeps me on the earth but i'm moving around a sphere so the question is. By how much does the curve of the earth drop to keep me on the surface of the earth after 8000 meters? So that i don't just fling out into space.

ANSWER:
I think you are just asking about geometry. Certainly, the curvature of the earth does not keep you from being flung "out into space"! You seem to be asking about the distance d in the figure here which is easy to calculate. If you go 8000 m along the surface, that is the arc length subtended by the angle θ. Therefore, θ=8000/R=8000/6.4x10⁶=1.25x10^-3 radians=0.0716º. Finally, you can write cosθ=R/(R+d) or d=R(1-cosθ)=5 m.

QUESTION:
What role do gravity or the weak nuclear force have in keeping the human body alive? Clearly, the strong nuclear force keeps us from dissolving into particles, but if you were suited up in between galaxies and gravity "disappeared", would the strong force be enough to keep us intact and alive? Also, electromagnetism is necessary for brain function (and heat transfer?), but do we use the weak nuclear force when making energy from food or anything like that?

ANSWER:
We evolved in a gravitational environment, so the proper functioning of many of our biological systems is dependent on gravity. Astronauts come back after long missions with weakend bones and muscles, for example. The electromagnetic force is probably the most vital because all of chemistry is electromagnetic. I cannot think of any biological functions which are directly dependent on the weak interaction.

QUESTION:
If g=GM/d ² then why does acceleration due to gravity decreases as we go deeper into earth?

ANSWER:
That equation is only valid for the acceleration outside a spherically-symmetric mass distribution. If you go inside the mass distribution, the equation is g=GM'/d ² where M' is the mass inside d.

QUESTION:
I did read one of your answers. I didn't quite get it. Electricity is electrons flowing through a electric field right? I had the problem, if electrons lose energy as heat etc. then some of the electrons energy must be lost. I thought it must be the electrical potential energy, since the electron is not losing kinetic energy. Because if it did lose kinetic energy, then the speed would reduce and that would reduce the current in different places of the circuit, which does not happen. Current in all parts of the circuit is the same. But you say, that the electron keeps bumping and has to start again and again, and that he moves real slowly. I thought the electrons were moving at light speed?

ANSWER:
I'm not sure which answer you read. This one is probably the best. Another good one to read is this one. So, to understand current you have to appreciate that it is statistical; there are such a huge number of electrons moving that all it makes sense to talk about is the average velocity of the electrons which is referred to as the drift velocity. When a collision with an atom occurs, kinetic energy is turned into heat energy. On average, electrons have constant kinetic energy but lose potential energy as they move along in the electric field. This energy lost to heat is supplied by the power source which is why you have to change batteries now and then or burn coal in a power plant somewhere to supply the energy. The drift velocity is, as explained in the second reference above, extremely slow, not the speed of light. When you turn on the potential difference, the electric field establishes itself along the wire at about the speed of light which is why a light seems to come on instantaneously.

QUESTION:
Why it is important for fission reactions to emit neutron ?

ANSWER:
Because a neutron can cause a fission to happen in another nucleus and therefore you have the possibility for a chain reaction.

QUESTION:
Do all weak interaction produce neutrinos ?

ANSWER:
Here is one which does not produce a neutrino. It does, however, involve a neutrino.

QUESTION:
Will two objects traveling in the same direction ever collide? Assume the objects are on earth, unmanned and their mass, volume, weight, density and speed are the same. All variables that can come in to play should be assumed that they are equal, for example no hills, curves bumps and no change in surfaces to have any effect on the coefficient of friction. Just a question my wife and I were wondering about.

ANSWER:
I'm not really sure what you are getting at here. If you are just wondering whether two parallel lines ever intersect, the answer is no. But you seem to want to know about material objects originally moving on parallel lines. To make the situation simpler, let's just have the two objects, originally with parallel velocities, move in otherwise empty space. If the original velocities are equal and they are traveling side by side, they will eventually collide because there is a gravitational attraction between them which will eventually bring them together. However, if they are originally side by side and traveling with unequal speeds, they would not collide if their relative velocities were greater than the escape velocity. The escape velocity for equal masses m originally separated by a distance r is v _escape=2√(mG/r) where G=6.67x10^-11 N⋅m²/kg² is the gravitational constant.

QUESTION:
A 400lb person jumps up 2-inches on earth. If same person jumps up on the moon, how high would the jump be?

ANSWER:
I will assume that whatever the jumper does will add the same energy on both earth and the moon. The gravitational potential energy U at the highest point must be equal to that added by the jump, and U=mgh where m is the mass (400 lb), h is the height (2 in on earth), and g is the acceleration due to gravity (9.8 m/s² on earth, 1.6 m/s² on the moon). The mass is the same both places, so h _earth g _earth=h _moon g _moon. Solving, h _moon=12.25 in.

QUESTION:
Hi, I was wondering what are the chances of survival from falling from the ninth floor of a building, going over the science of that how does surface affect the fall, body weight and trajectory. What is the difference from falling from a third story window as opposed to a higher up one?

ANSWER:
Someone else also asked this question; apparently it refers to a recent actual incident of a student falling out a dorm room window about 85 ft≈26 m high; the student survived without serious injury. The second person also wanted to know if I could estimate the force experienced on impact. First I will calculate the speed he would hit the ground if there were no air drag. The appropriate equations of motion are y(t)=26-½gt ². and v(t)=gt where y(t) is the height above the ground at time t, and g is acceleration due to gravity which I will take to be g≈10 m/s². The time when the ground (y=0) is reached is found from the y equation, 0=26-5t ² or t=√(26/5)=2.3 s. Therefore v=10x2.3=23 m/s (about 51 mph). The terminal velocity of a falling human is approximately 55 m/s, more than double the speed here, so the effects of air drag are small and can be neglected for our purposes of estimating. (If there is air drag, terminal velocity is the speed which will eventually be reached when the drag becomes equal to the weight.)

Estimating the force this guy experienced when he hit the ground is a bit trickier, because what really matters is how quickly he stopped. Keep in mind that this is only a rough estimate because I do not know the exact nature of how the ground behaved when he hit it. The main principle is Newton's second law which may be stated as F=mΔv/Δt where m is the mass, Δt is the time to stop, Δv=23 m/s is the change in speed over that time, and F is the average force experienced over Δt. You can see that the shorter the time, the greater the force; he will be hurt a lot more falling on concrete than on a pile of mattresses. I was told that his weight was 156 lb which is m=71 kg and he fell onto about 2" of pine straw; that was probably over relatively soft earth which would have compressed a couple of more inches. So let's say he stopped over a distance of about 4"≈0.1 m. We can estimate the stopping time from the stopping distance by assuming that the decceleration is constant; without going into details, this results in the approximate time Δt≈0.01 s. Putting all that into the equation above for F, F≈71x23/0.01=163,000 N≈37,000 lb. This is a very large force, but keep in mind that if he hits flat it is spread out over his whole body, so we should really think about pressure; estimating his total area to be about 2 m², I find that this results in a pressure of about 82,000 N/m²=12 lb/in². That is still a pretty big force but you could certainly endure a force of 12 lb exerted over one square inch of your body pretty easily.

Another possibility is that the victim employed some variation of the technique parachuters use when hitting the ground, going feet first and using bending of the knees to lengthen the time of collision. Supposing that he has about 0.8 m of leg and body bending to apply, his stopping distance is about eight times as large which would result in in an eight times smaller average force, about 5,000 lb.

Falling from a third story window (about 32 feet, say) would result in a speed of about 14 m/s (31 mph) so the force would be reduced by a factor of a little less than a half.

ADDED NOTE:
A rough estimate including air drag would have his speed at the ground be about 21 m/s rather than 23 m/s as above. Given the rough estimates in all these calculations, this 10% difference is indeed negligible.

QUESTION:
Does the gravity of the earth work through the moon? I.e. If you are on the "dark" side of the moon, do you weigh more than you would standing on the side facing the earth?

ANSWER:
Yes, the net gravitational field you see is due to all masses, not just the one you are closest to. On the far side of the moon the earth's field is weaker than on the near side, but it points in the same direction as the moon's field; so, you are right, you would be slightly heavier on the far side.

QUESTION:
Gravity makes Earth orbit sun, Milky Way and Adromeda collide with each other,etc... My question is, what can provide the necessary energy for a system like this for billions of years?

ANSWER:
The earth orbiting the sun has energy, but it takes zero energy to keep it orbiting. The Milky Way and Andromeda galaxies have energy but no additional energy is added as they move toward each other and eventually collide.

QUESTION:
If I use some magnetic bars, cut them perfectly so that I can put them together to form a globe, with the same pole pointing outwards, and the other pole pointing inwards, do I get a Magnetic monopole object?

ANSWER:
Think of your bars as dipoles of positive and negative magnetic charges (monopoles) separated by a distance d. The magnitude of the magnetic field B of a monopole is inversely proportional to the square of the distance r from the charge, B=kq/r ² where k is some constant. In the drawing above the field at point p is B=B _-q +B _+q =kq[(1/(r-d)²-(1/r+d)²]=4kqrd/[(r+d)²(r-d)²]. Now, look at the field when r>>d: B≈4kqd/r ³. The field does not look like a monopole because it falls off like 1/r ³, not 1/r ².

QUESTION:
It might look like a homework question, but it is not. Please help me. I have asked this question everywhere I could, but everybody seems to ignore it. So, the problem is: Let us say we have two bodies A and B in contact with each other, with A lying at the back of B, and the system is on a friction-less horizontal surface. Let A have mass 5 kg and B 10 kg. Now let's say I apply a force of 45 N on A with my hand, then the system begins to accelerate at 3 m/s^2 and the net force on B by A is then 30 N, and B in reaction applies a net force of -30 N on A. Thus, the net force on A is 15 N. What I do not understand is why A is not applying a force of 45 N on B? If it is due to the reaction of B on A, how does A know in the first place that it is to exert a force of 30 N on B so that it receive a reaction of -30 N from B? Is not the reaction force of B on A some kind of a function of the action of A on B, and if it is, then how is the magnitude of the action of A on B is first determined? What is it that I do not understand about Newton's Third Law of Motion?

ANSWER:
OK, I will take your word for it that it is not homework. It is important to be able to solve these kinds of problems. My method is to choose a body and look only at that body. I choose first (as you did) to choose both masses as the body, so M=15 kg and F=45 N and therefore a=F/M=3 m/s². Next I choose B as the body. The only force on it is the force which A exerts on it, F _BA. Since we know that m _B=10 kg and a _B=3 m/s², F _BA = m _B a _B =30 N. Finally choose A as the body. Two forces act on A, F=45 N and the force which B exerts on it, F _AB=-F _BA=-30 N; its mass is m ₅=5 kg and therefore a=(F+F _AB)/m ₅=(45-30)/5=3 m/s². The reason that there is not a 45 N force on B is because your finger is not touching B, only A is touching B. The reason A "knows" to exert a force on A is that it has no choice since A's acceleration and mass are already fixed. Once you know the "reaction" force you automatically know the "action" force because of Newton's third law, F _AB=-F _BA=-30 N for this problem. You could also have chosen A as the body before you chose B as the body. Two forces act on A, F=45 N and the force which B exerts on it, F _AB. Its mass is m ₅=5 kg and its acceleration is 3 m/s²; therefore (45+F _AB )= m ₅ a=15 N or F _AB=15-45=-30 N.

QUESTION:
I'm bothered by the seeming interchangeability in physics of the terms 'measurement' and 'observation'. Scenario: Doing a double slit experiment while firing one electron at a time - in a darkened room with a person "observing the experiment" and one without an observer. And also doing another set of experiments with and without a detector - are the results different? if so, how?

ANSWER:
There can be confusion but it is mainly semantic. If you simply "observe" the double slit experiment by counting electrons which hit the screen and determining where they hit, no "measurement" has been made regarding the double-slit experiment itself, you have simply observed how the results play out after the electrons pass through the slits. However, if your observation includes some apparatus to determine through which slit each electron passed, that is a "measurement"; in that case, the measurement will destroy what you previously observed—the interference pattern.

QUESTION:
Are star wars blaster weapons possible? i know lasers wouldnt work because its just light but maybe plasma energy or energy projectiles could work? i just need to know if the blaster rifles/pistols as pictured in star wars and the way they function could EVER work in the distant future and what way you think they could possibly work, assuming we had all the technology necessary to do so. thank you in advance for your knowledge.

ANSWER:
First of all, they are fictional with not much information available regarding their power. However, a quick search of the web reveals that many Star Wars enthusiasts have tried to make estimates of their properties from detailed examination of the movies. First observation is that they are not lasers because you can see their trajectories and Han Solo is seen to jump out of the way in time to not get hit; light is just a lot faster. (You should not write them off just " … because it's just light … " light, though; lasers can melt steel.) Also, if the pulses are any kind of material (super-heated plasma, charged particle beams, etc.), they could not propogate very far in air which they do. But the thing that makes them, in my view, impossible is the energy each pulse carries on the highest setting; one site I found estimated the energy of a single pulse to be on the order of several megajoules. Suppose that a single pulse lasts 1 ms=10^-3 s and carries an energy of 1 MJ=10⁶ J; the power carried by that pulse would be 10⁶/10^-3=10⁹ W=1 GW. This is the power output of a typical power plant. Where are you going to get this kind of power in some compact form you can carry around with you? No way!

QUESTION:
When in the early universe did life become possible? I'm assuming it would have had to have been at some point when the temperature had cooled down enough so that the protons and neutrons of basic elements of life like carbon and oxygen could bond and come together. Also, what do you believe is the purpose for intelligent life in the Universe?

ANSWER:
I usually do not answer questions about astronomy/astrophysics/
cosmology as stated on the site. I can give you a little information here, though. The universe just after the big bang was almost exclusively hydrogen. No elements which could be used to form planets where life might develop or the material for life itself. The first stars started forming about 100 million years after the big bang, basically pure hydrogen stars. These had to be much larger than the sun (perhaps 300-1,000 times heavier) because of the lack of heavier elements and consequently their lifetimes were too short (a few million years) for life to evolve (it has taken about 5 billion years to reach our stage of evolution, about half the sun's lifetime). Inside these stars nuclear fusion caused heavier and heavier elements up to about iron to form; then when those stars used up all the fuel, they exploded (super novae) scattering the heavier elements to eventually be part of clouds of dust and hydrogen which subsequently formed new stars with the possibility of planets. (As you can see, it is not "cooling down" which is responsible for heavier elements which are created in stars which are super hot.) So, we are now at least several billion years into the age of the universe. More detail on early stars can be read in a Scientific American article. The "purpose" for anything is not within the purview of physics.

QUESTION:
I want to design a home-built experiment that will physically display the actual curvature of the Earth, and I would appreciate validation that my methods are (at least theoretically) - scientifically accurate. This test is based on the geometric relationship of a tangent line (globally 'straight' line) when it is perpendicular to a radial line of the sphere. . I am going to set 51 fenceposts fifty feet apart for a total length of 2500 feet. I'm going to use a water linelevel to mark a "locally' level line on the first two posts. Then, using a laser light as a straight-edge, I will extend this straight line for the full 2500 feet. Then I will take the water linelevel to the last two posts, hold the level to the straight line marks, and note that the globally straight line is now an inch and 3 quarters out of "local" level, due to the Earth's curvature. . This inch and 3 quarters divergence is derived from the formula for the Earth's curvature that is eight inches per mile squared: 2500 feet is .4734 of a mile. Squaring that, then multiplying by 8 inches, gives 1.7931 inches. . Any advice or criticism or insight you could offer would be well appreciated. For brevity's sake I kept this desription quite short, but I will be happy to elaborate in greater detail if you want me to.

ANSWER:
Here is the problem: You assume that the earth is a perfect sphere. It most certainly is not, particularly at the half-mile level. You can see some detail in a calculation I did in an earlier answer about the Bonneville Flats where a similar question to yours was looking to observe curvature at the 10-mile level. It takes several hundred miles to be able to do an accurate measurement of the earth's curvature; the ancient Greeks did this around 200 BC.

QUESTION:
If I am running at average sprinting pace for an 17 year old male and I jump off of a 80 meter drop, how far forward will I land from the jumping point? Assuming I am around 11 stone.

ANSWER:
80 m is pretty high, so you will be going very fast when you hit; therefore, neglecting air drag might introduce significant error. But air drag is pretty tricky to calculate and I will neglect it; the answer I get will be somewhat bigger than what would really happen. I will take your speed to correspond to running a 100 m dash in 15 s, about v ≈6.7 m/s. The equations of motion are x=6.7t and y=-4.9t ² where x and y are the horizontal and ver tical positions relative to the edge of the cliff and t is the time after jumping. Solving the y equation for t when y=-80 m (the ground), t=√(80/4.9)=4.04 s, so x=6.7x4.04=27.1 m. That is the answer neglecting air drag. Note that it is independent of the mass m.

QUESTION:
We represent waves by crest and troughs like ( ups and downs ) but in the slit interference process we represent it in the form of other figures like ))))))) . can u tell me how crests and troughs are represented in this form ?

ANSWER:
"...figures like )))))..." are called wave fronts. Each front is meant to represent the locus of points at some instant where the wave crests are and halfway between are the wave troughs.

QUESTION:
According to Einstein,gravity is the bending of space-time by matter which is unlike Newtonian gravity.But there are boson particles called gravitons which are thought to be the cause of gravity. Aren't these theories conflicting?How can gravitons exist if there is no gravitational force?

ANSWER:
It is generally believed that gravity, like any other field in physics, should be quantized. So far, there is no successful theory of quantum gravity. If there were such a quantized gravitational field, there would be a boson "messenger" like the photon for the electromagnetic field or the gluon for the strong interaction field; that would be the graviton. Since there is no theory, there is no graviton, only speculation.

QUESTION:
Many explanations in physics which I have seen proceed with a 3D Euclidean space, empty but for a population of objects. Lines representing electromagnetic radiation are drawn from emitter to sensor to explain various phenomena. The apparently discreet nature of the representations leaves me wondering - When I see a star, I see it "everywhere", there seem to be no black spots . Spokes radiating from a wheel grow farther apart as they proceed, why not light from a star? Be it particle or wave or some probabilistic combination, does not some m/e travel from the star to strike my eye? Why does this not put the burden of infinite m/e on any light source?

ANSWER:
Those "rays" you see drawn in geometrical optics are not meant to represent the only place light is. There is no rule about how many rays to draw but the direction of a ray is always the direction that light is traveling at any point on the ray and the intensity of the ray is implicit in the density of the drawn rays. The rule for how to draw a ray between two points is that you find the path which will take the shortest time. For a point source of light (like a star) in a vacuum (approximately what is between you and the star) that will be a straight line. In the picture above you could have drawn twice as many rays and that drawing would still have conveyed the same information about the light. An alternative way to represent the waves is to draw wave fronts which are concentric about the point source and equally spaced; these are meant to represent the location of the crests of the light waves at some instant and are imagined to be expanding outward from the source. The rays are always normal (perpendicular) to the fronts. This drawing is really a cutaway because the fronts are really spheres, so you see that wherever you stand you will see light. Because a wave front is expanding, its area (4 πR ²) is getting bigger so the energy of that wave is getting more and more spread out meaning that the light is getting dimmer.

QUESTION:
I have a question about the properties of light. If I am traveling at 99.99999... The speed of light and shine a light in the exact opposite direction, how would that light behave to an observer? Would it stay still? Would the light still travel at c?

ANSWER:
Every observer measures the same speed of light, c. That does not mean that the light is identical. If the source has a huge speed, the light has a huge red shift, its wavelength is greatly larger than that observed if at rest relative to the source. It would likely be invisible to the unaided eye.

QUESTION:
I have 300 grms of baked beans that I want to heat in a microwave. Wil it take longer or more energy to cook these beans in one dish or in separate dishes of 150grms each?

ANSWER:
The rate at which the beans will be heated by the radiation (R _H) is proportional to their volume. But, as soon as they start heating up, they start cooling off by radiating from their surfaces; the rate of cooling (R _C) is proportional to the area. Roughly speaking, the volume is proportional the the L ³ and the area is proportional to L ²where L is a measure of the size of the pile of beans. The ratio R _H/R _C=KL ³ /L ²=KL determines the net rate of heating; K is some constant. For example, suppose your beans were contained in a spheres of radii L and 1.26L; I chose those because the larger radius sphere would have twice the volume of the other. Then, the larger sphere will heat up 1.26 times faster than the smaller (two spheres). Assuming that the microwave energy is constant with time, the longer time it takes the more energy is used.

The problem with my analysis, though, is that it depends on the power of the microwave. If it has a relatively low power, the radiation will be mostly absorbed in the beans and the assumption that R _H is proportional to the volume becomes untrue. Only if a small fraction of the radiation is absorbed by the beans will my analysis be approximately correct. You should do an experiment, try it!

QUESTION:
Why only magnetic moment due to spin is considered in proton nmr spectroscopy. what about magnetic moment due to orbital motion??

ANSWER:
You are right, a proton in a nucleus will have both spin and orbital magnetic moments. But the whole idea of NMR is to put magnetic moments in a magnetic field and they tend to align. To flip the spin requires a certain amount of energy. So you send photons of the right energy, typically radio frequency radiation) and they will flip the proton spin. You need not worry about other moments because the photons are tuned only to the right frequency for spin.

QUESTION:
In understanding that two objects (no matter their phisical properties) will accellerate at the same rate towords the same gravitational force in a perfect vacuum, do we take into consideration the gravity of the falling objects themselves? Would the larger gravitational force of the larger falling object be perfectly offset by the larger ammount of inertia or tendency to resist motion?

ANSWER:
The force F between masses M and m whose centers are separated by a distance R is F=GMm/R ². But, the acceleration a of m is a=F/m=GM/R ². So, as you ask in your last sentence, the inertia (m in a=F/m) cancels out the mass (m in F=GMm/R ²) in the acceleration. This is actually a profound finding for the following reason. In Newton's second law, mass is, as you say, inertia (inertial mass, m _I); in Newtons universal law of gravitation, mass is the ability to feel or create gravity (gravitational mass M _G). The fact that gravitational accelerations are the same implies that m _I=m _G, not something you would necessarily expect. Why these are equal was not really understood until the general theory of relativity was proposed by Einstein.

QUESTION:
i am a metal worker and maybe it's dumb but i have thought up an idea for renewable energy. I need to build a huge tank capable of holding 10000 of water, it will have a coned base with a hose coming off it and running back up into the tank, returning the water to it's point of origin....question is...with 10 tons of water down force, 1 meter from the ground....would a decent amount of water travel up that hose pipe and back into the tank???..

ANSWER:
It makes no difference if you have a whole ocean of water, the water at the bottom can never push water higher than the surface of the tank, can never cause a continual current like you envision. There is a very detailed answer for a very similar question to yours that you should look at.

QUESTION:
In the event horizon of the black hole, a pair production of a particle and an anti particle and the falling of one into the black hole and the releasing of the other from it gives us the Hawkins radiation, but my question is , isn't it possible for both the particle and the anti particle to fall into the black hole. If that happens defiantly the vacuum energy of the space decreases how can the universe compensate this decrease in energy to validate the law of conservation of energy.

ANSWER:
There are two ways you can imagine the creation of the particle-antiparticle pair (PAP):

Vacuum fluxuations where a particle-antiparticle pair is spontaneously created just outside the event horizon, violating energy conservation. However, the uncertainty principle (UP) allows this violation but only for a very short time. If one escapes, it adds energy to the universe so the captured particle must have negative total energy thereby decreasing the mass of the black hole and maintaining energy conservation. If both particles are captured, they are required by the UP to recombine thereby keeping the mass of the black hole constant.
When a virtual pair is created just outside the event horizon, the intense gravitational field of the black hole can provide the energy for the PAP to become real rather than virtual. In this case, the energy acquired by the pair will be lost by the black hole reducing its mass. If only one of these is captured, the energy of the escaped particle will be added to the universe but the energy of the captured particle will be added to the (already reduced) energy of the black hole resulting in a net loss of energy of the black hole equal to the energy of the escaped particle.

Energy of the whole system is conserved.

QUESTION::
If the speed of sound is inversely proportional to the density of a material, why does sound travel faster in solids (it is the most dense). I have read that it takes more energy for sound to travel in dense materials so it takes longer but then neighbouring molecules are closer so sound does not have to travel that far, making it faster. This doesn't make any sense because it says the more dense a medium is, sound is both faster and slower. Also, how does bulk modulus affect the speed of sound.

ANSWER:
You are oversimplifying because the density ρ is not the only thing which determines the speed of sound. In general, the speed of sound v may be written as v= √(K/ρ) where K is a parameter which specifies the "elasticity" of the material. (Note that v is inversely proportional to √ρ, not ρ as you state.) For example, just qualitatively, you might say that steel is much denser than air but it is also much more elastic. The way K is specified for gasses is quite different than for solids. For an ideal gas, K=γP where P is the pressure of the gas and γ=5/3 for monatomic gasses and 7/5 for diatomic gasses. On the other hand, for solids K=B+4G/3 where B is the bulk modulus and G is the shear modulus. For solids K is enormously bigger (~10¹¹ N/m²) than γP for gasses (~10⁵ N/m²). That answers your question. So, let's just do a rough calculation to see if I get reasonable values for air and steel:

Taking air as mainly diatomic γ≈ 7/5 , atmospheric pressure P≈10⁵ N/m², ρ≈1 kg/m³, v ≈374 m/s; a little high, but close.
For steel, B ≈1.6x10¹¹N/m², G≈7.93x10¹⁰ N/m², ρ≈7900 kg/m³, v≈5800 m/s; this is exactly the speed of sound in stainless steel!

QUESTION:
The earth's radius varies depending on latitude. How many times greater is the acceleration of gravity at the poles of the earth than the equator if the radius of the earth is 99.5% smaller at the poles than the equator?

ANSWER:
To calculate exactly would be impossible because the earth is not a perfect spheroid and its mass is not uniformly distributed. But you can get a good idea by calculating the difference in gravitational force for spheres of the same mass but having the two different radii; these radii are 6378 km (equator) and 6357 km (poles), about 0.33% larger at the equator. Since the gravitational force is inversely proportional to the square of the radius, this would give about a 0.11% smaller g at the equator. This effect is smaller than the effect due to the earth's rotation which results in about a 0.34% reduction at the equator (due to centrifugal acceleration).

QUESTION:
What is the purpose of utilizing a percentage of body weight to determine how much weight to bench press/push/whatever? I know this seems like a fitness question and not a physics question, but what I am interested in is WHY weight would be used to determine how much one could (or should be able to) lift/push? For example: A gym teacher wants to grade his students on their strength. He decides to use abililty to push a weighted sled across the floor as the measure. He wants to make the task equally difficult for every student in order to make the grading fair. So, he decides that each student will push 2x his/her body weight for 5 minutes and the grade will be based on how FAR the student is able to push. So, Student A weighs 170 pounds and pushes 340 pounds (including the weight of the sled) for a total of 160 yards. Student B weighs 240 pounds and pushes 480 pounds (again, including the weight of the sled) for 80 yards. Student A pushed farther and gets a better grade, but Student B complains that he had to push much more weight so he should not get a worse grade. Does Student B have a legitimate complaint or does his heavier weight contribute somehow to his ability to push that doesn't have anything to do with his strength? As in, does his weight help push the sled in some way? Sorry, I don't know enough about physics to ask this question using proper physics terms like force, mass, etc. I hope you will still answer my question!

ANSWER:
I cannot comment on the rationale for correlating weight to strength. I can certainly comment on the physics of your particular example of sled pushing. I would first of all comment that this example is certainly not one solely of strength because, since it is a timed activity, endurance as much as strength is being tested; if one student, for example, were a heavy smoker, he would likely become exhausted more easily. As a physicist, I would equate "strength" with force. The specific example you give, though, seems to me to be more related to energy (work done by the student) or power (rate of energy delivered) than strength; purely in terms of strength, the heavier student exerts more force. The force F which each student must exert depends on the weight w he is pushing and the coefficient of friction #956; between the sled and the ground, F= μw. The work W done in pushing the sled a distance d is W=Fd= μwd. The power generated if W is delivered in a time t is P=W/t=μwd/t . Both students have the same μ and t , so W _A/W _B=P _A/P _B=d _A w _A/d _B w _B=(160x340)/(80x480)=1.42. So student A did 42% more work, generated 42% more power, than student B. From a physics point of view, B demonstrated more strength, A demonstrated more power. I would judge that this is not a fair way to assign a grade. It would be interesting to see if A (B) could move B's (A's) sled 80 (160) yards.

QUESTION:
Say I have 2 factories producing an object, we'll be arbitrary and say bottle caps. Each produces them at a rate of 1 per second. Now ignoring things like raw materials etc... One stays on Earth, producing its bottle caps constantly. The second one (somehow) gets accelerated to (again being arbitrary) 90% the speed of light and remains at that velocity until completing a round-trip 100 years long. When the moving factory returns, 100 years later from the perspective of the factory on Earth...will there be a difference in the total number of bottle caps each has produced?

ANSWER:
This is just a variation of the twin paradox. The number of bottle caps produced by the moving factory will be N √(1-0.9²)=0.44N where N is the number produced on earth.

QUESTION:
Okay, so for a while I've been wondering why bass travels through certain materials that higher frequency sound doesn't. I have a theory which could be wrong but what I thought is that bass, having a larger wavelength, passes through particles that are bigger, and that shorter wavelengths can't get through. Somewhat like red light and blue light traveling through the atmosphere. Okay, so I looked it up everywhere (almost) and couldn't find a straight answer, even my physics professor didn't know surely why this happens. So, maybe you could. Why can I hear just the bass when someone blasts music in their car?

ANSWER:
The reason is that the attenuation of sound intrinsically depends on the frequency of the sound, the higher the frequency the greater the attenuation. The theory of attenuation is rather complicated, so I will just sketch the results. For a Newtonian fluid, Stokes showed that A(d)=A ₀e^- ^αd where A(d) is the sound amplitude a distance d into the material, A ₀=A(d=0), and α= 8 π ² η f ² /(3ρv ³); here η is viscosity of the fluid, f is frequency of the sound, ρ is the density of the fluid, and v is the speed of sound in the fluid. The important thing to notice is that the amplitude decreases like exp(-βdf ²) for any Newtonian fluid. For example suppose you compare f ₁=20 Hz with f ₂=1000 Hz for a thickness of d=1 cm=0.01 m and A ₁(0.01)=јA ₀=A ₀e^{-β�0.01�400}=A ₀e^-4β which can be solved for β, β=0.35 s²/m; then, for f ₂, A ₁(0.01)=A ₀e^{-0.35�0.01�1,000,000}=A ₀e^-3500 = A ₀x 9x10^-1521≈0. Finally, for any material, Stokes' law of attenuation still may be written as A(d)=A ₀e^- ^αd except α=βf ^εwhere 0<ε<2. Water and most metals have ε≈2. But even if ε is smaller, it is always positive which means that the attenuation is always greater for a higher frequency.

QUESTION:
We know the relative size of the solar system measuring thru the distances of the planets circling our star. Do we know the thickness of this rotational disc? Is the gravity of our star concentrated only on this single orbital plane as our star rotates? If not, why do planets not circle verticaly as well as on horizontal planes? As far as I know we have only sent space craft thru our orbital disc towards other planets. Do you believe if directed a flight up from our orbital plane would the suns gravity lessen where our space craft could fly faster?

ANSWER:
I should first address your speculation that gravity is stronger on the disc near which the planets orbit. In fact, gravity depends only on how far you are from the source, so if you went 100,000,000 miles from the sun in any direction you would find the same gravitational force. There is not really any well-defined disc whose thickness you can measure; all the planets are nearly all orbiting in the same plane and the inclinations of the orbits relative to say, the plane of the earth's orbit, are all less than 3 Ѕ⁰. But that does not mean that everything is near that plane. Many of the dwarf planets are much out of the plane of our orbit; Pluto, for example, is about 18⁰ inclined relative to our orbital plane. Outside the most distant planets is the Oort cloud, a collection of rocky and icy bodies which is distributed roughly equally in all directions; comets are thought to originate in the Oort cloud and when they enter the inner solar system they come from all directions relative to the orbital plane. The reason that the planets are all nearly on the same plane is that when the sun first formed from a huge cloud of dust and rocks, it had angular momentum and as the system collapsed under its own gravity, it spun faster and faster and the resulting centifugal force caused it to flatten like a giant pizza dough.

QUESTION:
An image is formed when the reflected ray meet each other at a point. But why does an image is not formed by the intersection of incident rays? After all they are the same light rays and it's not like there's some kind of reaction which takes place or something.

ANSWER:
The light rays from each point on the object all diverge away from that point. Unless there is something to change their directions, e.g. a mirror or a lens, they never meet.

QUESTION:
If I were to throw a pencil up into the air, would it come down at the same speed as I threw it up?

ANSWER:
It would if there were no air. However, air drag takes energy away from the pencil and so it would arrive back at your hand going more slowly. For speeds you are likely to be throwing the pencil, though, this effect is small and often neglected in elementary physics classes.

QUESTION:
The demonstration wherein one pours water from a clear vessel and one shines a laser pointer (a red laser pointer in my case) through the water and it appears the laser beam bends with the water pouring out of the clear vessel; What causes the beam to bend with the water? Would this same type of effect work with other fluids than water, such as air or glass?

ANSWER:
It is caused by total internal reflection. If the angle which the light hits the surface between the water and the air is glancing enough, the light will be reflected back into the water rather than be refracted into the air. Total internal reflection can happen whenever light strikes the interface with a material of smaller index of refraction; the minimum angle for which it can occur depends on the relative indices of refraction.

QUESTION:
I was reading a introductory book on particles. I read that neutrinos only respond to weak and gravitational forces, isn't that fact that it responds to gravitational forces prove that it has mass? So why was this years Nobel Prize awarded for figuring out that neutrinos had mass?

ANSWER:
No, responding to gravity does not imply mass. Photons, which are known to be massless, are deflected when passing near a large mass. See FAQ page.

QUESTION:
If a train runs at 100km/h and if in this train somebody drops a rubber ball and catch it, let's say it drops down 1m and up in one second, it means that the ball has travelled 2 meters in one second for the person in the train. If I am at the station looking at the train when it passes me by and let's say it is made of glass so I can see what is happening, I can see the ball dropping down and up but for me as the train is moving the ball will have travelled 2 meters plus the distance travelled by the train in one second so more than 2 meters. I don't think that space time dilatation plays at this sort of speed so how is it explained?

ANSWER:
Actually, you have not calculated the distance traveled correctly. But because the ball is speeding up on its way down and slowing down on its way up, you have set up a problem with unnecessarily difficult mathematics to calculate the distance seen by the person at the station. I will alter your problem somewhat to make it easier to calculate: the ball is made to first move down at constant speed and then to move up with the same constant speed. If the time is still 1 s, the necessary speed is v _y=2 m/s. The train is moving with speed v _x=100 km/h=27.78 m/s so the ball and train move a distance 27.78 m horizontally during the one second the ball is moving. But the distance the ball moves is not 27.78+2=29.78 m but rather 2√( 13.89 ²+1² )=27.85 m because the ball will take a zig-zag path. But the ball also has a different speed as seen from the station, v=√ (v _x ²+v _y ²)=27.85 m/s. We therefore conclude that the time it takes the ball to travel 27.85 m is 1 s, so everything hangs together. Your error was to ignore the fact that the ball has a horizontal component of its velocity in the frame of the station. You are right that relativity plays no role here.

QUESTION:
Suppose I have a charge +q and there is a point P , Suppose I place a conductor between the charge +q and P . Since there are free electrons in it , Negative electrons move towards +q and equal positive charge inside the conductor near P , The conductor has charge distribution like a dipole. So If I want to calculate E field at P . I could use superposition principle to find E at P due to +q and E due to dipole. But Gauss's law says that dipole doesn't contribute anything to E field at P. Can you explain me 'intuitively' (Not in equations) why the dipole wont contribute anything to the field at P ?

ANSWER:
Gauss's law does not say that the dipole contributes nothing at P. If you put a spherical Gaussian surface enclosing both q and point P the net charge enclosed is q but that does not mean that the field due to the dipole is zero everywhere on that surface. All you can say is that the net electric flux passing through that surface is q/ ε ₀. Gauss's law is usually useful in determining a field only if the field can be argued to have constant magnitude and normal to the surface everywhere. Superposition, not Gauss's law, should be used for this problem.

QUESTION:
If I was in a spaceship moving at half the speed of light (in normal space) and I measured the time it took the beam of light from a laser pointer to travel from its source to two points inside my ship, one in the direction of travel and one in the opposite direction, wouldn't C demand that I observe different time measurements? If the time measurements are the same, then when I pointed in the direction of travel, the light would have to be traveling at C plus the speed of the ship from observations made outside of the ship. If the measurements are different, then shouldn't we be able to observe the same effect on earth because of the direction of travel of our planet, solar system, Galaxy, and group of galaxies?

ANSWER:
I am not sure what you are asking here. Does this earlier answer help you? One thing is clear is that you do not really appreciate that the speed of light in vacuum is independent of the motion of either the observer or the source. This is one of the main postulates of special relativity. See the FAQ page for questions related to this.

QUESTION:
Sir,I am a mechanical engineer by profession but very interested in reading physics fundamentals. Recently I went through the fundamentals of electro magnetism and I got this doubt. Consider two charges each of charge +q rigidly fixed in a train moving with a constant velocity, V. Let the train speed be negligible compared to speed of light so that we can treat the problem in non-relativistic terms. The fixity condition ensures that it overcomes electrostatic forces and remain motionless. A traveler in train sees both of them at rest and there wont be any magnetic forces developed between the charges. Now consider an observer in platform. For him, both charges are moving with a constant velocity, V equal to the train velocity. Each charge will develop magnetic field according to this observer as per Biot-Savart law and there will be mutual attraction as each charge is moving under the magnetic field of other.Thus, an observer in train sees no magnetic forces whereas an observer in platform sees mutual magnetic attraction. How do you explain this?

ANSWER:
There is no rule which says that the either the electric or magnetic field must be the same in all frames of reference, even slowly moving frames like you specify. The real root of your problem is that electromagnetism is intrinisically relativistic, even at slow speeds; the electric and magnetic fields of classical electromagnetism are really both components of the electromagnetic field which is a tensor and when you change inertial frames, you cause a transformation of that tensor into another where both the electric and magnetic field pieces of it are different. In your second case you would also find that the electric fields were slightly different from their original values but the differences would be very tiny; the magnetic fields, though, are nonzero but small, but small is very big compared to the original magnetic field of zero.

If you are interested, I will give here the electric and magnetic fields for one of the charges moving with velocity v in the +x direction. E' = iE _x+ γ( jE _y+ kE _z) and B'=-( v x E' )/c ²where γ=1/√[1-(v/c)²] and i , j , k are unit vectors; the vector E is in the frame where q is at rest and E' and B' are when q is moving.

QUESTION:
I see the equations for computing the slowing of time, based on speed compared to light speed. Do we always use c=3^10 cm/sec? I am asking since light speed is slower, sometimes much slower, in mediums other than air or space. If we use a smaller value for c, the time dilation factor is enhanced.

ANSWER:
The significant thing in the theory of special relativity is the speed of light in vacuum. What matters in the theory is the universal constant c, not the speed in the medium you happen to be looking at.

QUESTION:
Is it true that a person flying in an airplane is actually living a shorter amount of time, than a person standing on the ground?

ANSWER:
You must specify " … living a shorter amount of time … " with respect to whom . The person in the airplane sees time progressing at a normal rate. However, the person on the ground will see the clock of the person on the airplane run slowly, so he will perceive the traveling person to be " living a shorter amount of time", i.e. she will have aged less when she returns to earth. You should read FAQ Q&As on the twin paradox, how clocks run, and the light clock.

QUESTION:
If I was travelling in a bus and the bus was travelling at around 60 mph and I jumped in the air, how come I don't fly to the back of the bus. Like with flying, if I was in an airplane travelling at around 500 mph, and I was floating without an aid in the cabin why do I travel with the plane not just get smashed to the back?

ANSWER:
It is impossible for you to be " floating without an aid ", so let's assume that you are standing on the floor of both the bus and the plane. In both cases it is because of Newton's first law. Someone watching you from the ground would see both you and the vehicle as moving with the same speed. From that point of view you are in equilibrium because the only forces on you are your weight down and an equal force up from the floor. Newton's first law says that if you are moving in a straight line with constant speed you will continue to do so if all forces are in equilibrium. When you jump up, the floor no longer exerts a force on you, so you are no longer in equilibrium vertically and you will fall back to the floor. But you are still in equilibrium horizontally (there are no forces on you horizontally) so you will continue, right along with the bus or plane, to move horizontally with the same speed. Actually, I did this the hard way because Newton's third law will still be valid in the moving bus or plane, so when you jump up you will not move horizontally because there are no forces which act horizontally on you to accelerate you (make you start moving horizonatlly).

QUESTION:
If I have two soccer balls the same size, yet one is heavier than the other, which one will go farther with the same kicking force involved? How does momentum and Newton's Second Law come into play here?

ANSWER:
I will assume the balls fly through the air, not roll or slide on the ground. This question has no single answer. Before getting too deeply into this, I need to modify your question a little. The force does not determine what happens to the soccer balls (see FAQ page), so let us change " same kicking force" to "same kicking impulse"; impulse is essentially force multiplied by the time it was applied. That is also more convenient because the change in linear momentum (mv) is equal to the impulse (J). So, with equal impulses, the lighter ball has a larger initial speed: v _light=(m _heavy/m _light)v _heavy. So, if both balls are launched at the same angle and if air drag can be neglected, the lighter one will go farther because it started with a larger speed. Maybe that is all you wanted. But, it is altogether possible that air drag will not be negligible. The force of air drag may be roughly approximated as F=јAv ²for a sphere where A is the cross-sectional area of the balls. (This is true only for SI units since ј is not dimensionless.) So now you see that the ball launched the fastest experiences the larger air drag slowing it down. But the heavy ball has even more advantage since Newton's second law says a=F/m so even if the two balls experienced the same force, the less massive ball would have a larger magnitude of acceleration, slow down faster. Now it becomes complicated because you have to know the masses, the impulse, and the angle of the launch to calculate which would go farther.

QUESTION:
Let's say you have a very long strong tube uncapped at both ends, and laying at sea level. It would have one atmosphere pressure inside. Put a cap on one end and stick that end down to near the bottom of the Mariana Trench. Now pop the cap off. Wouldn't this create a perpetual geyser from the end at the surface? It seems to me that it would come out with enough pressure to run a generator. Would it be considered perpetual motion or just hydraulics? Why wouldn't this set-up solve the world's clean energy needs? Please pop my bubble. I can't be the first to think of this. What am I not accounting for? Inside the tube I don't think gravity would be a player. Neither would the pressure fading outside the tube.

ANSWER:
Once the water reached the top of the tube the column of water would be in equilibrium, just the same as if you had put the tube down without capping the bottom. You might get a spurt at first but then you would just be left with a column of water in equilibrium. I guess you could analyze it roughly by ignoring viscosity and the drag of water moving on the pipe. Suppose the cross-sectional area of the tube were A, the depth of the bottom is D, and the density of water is ρ . At some time after uncapping, the distance up to the current level of the water in the tube I will call z. The force up on the column of water would be F _bottom=(P _atm+ρg D ) A, the weight of the column of water is W=ρgzA, and the force down on the top is F _top=P _atm A. The net force on the column is F= ρgA (D-z)=ma= ρAza where a is the acceleration and m= ρAz is the mass. So, a= ρgA (D-z)/ ρAz=g [(D/z)-1]. Suppose we take g≈10 m/s² and D≈10⁴ m; then a≈10[(10⁴/z)-1] m/s². The graph of the acceleration is shown to the right; note the logarithmic scale for acceleration to show the huge variation from bottom to top. Note that it is huge, about 10⁵ m/s² for 1 m and falls by four orders of magnitude when the column of water is halfway to the surface, finally falling to zero when the pipe is full. Suppose we start with z=1 m and the column at rest (where a≈10⁵ m/s²). After 10 milliseconds (10^-2 s) the column will have acquired a speed of approximately v=at=1000 m/s and the water level would have risen approximately to z=1+Ѕat ²=6 m. Now, the speed is almost immediately huge and so the assumption of no frictional forces becomes impossible. The drag of due to the water moving in the tube for the column of water going 1000 m/s will be huge and keep the water from speeding up so rapidly. Also, the air above the column of water will not just get pushed up will get compressed and therefore push down on the column with a pressure greater than atmospheric. It is therefore clear that my simple calculation above is only a best case scenario and the drag and added pressure will take energy away. The drag might get big enough that the water in the tube would boil and release steam to futher impede its progress. I believe that you will end up with column of water slowing down as it approaches the surface of the ocean and it will just come to rest there. In any case, when the tube was filled, even if still moving, the column of water would have zero net force on it. If you tried to have it do work on your turbine, it would soon loose all its kinetic energy and stop. Alas, no clean energy solution!

ADDED THOUGHT:
Robert M. Wood pointed out to me that the most energy you could possibly get out of the rising water would be the amount of work you performed to get it down there. If you neglect the weight of the tube itself (or, imagine first lowering the tube open at both ends and then pushing the water down with a piston), this work would be W=ЅρgAD ². Neglecting any energy loss, this would have to be equal to the kinetic energy of the column of rising water when it got to the top, K=ЅρDAv ², so v=√(gD). For the case above, v=316 m/s, pretty modest. And keep in mind that all the water in the tube is now in equilibrium, so as the water goes above the surface, it is slowing down as it gains potential energy. And, if you imagine the tube projecting high above the surface, you can calculate how high h the water will rise before falling back. The center of mass of the column of stopped water is y=Ѕh and its mass is ρhA, so mgy=Ѕh ² ρgA=ЅρDAv ², so h=v√(D/g)=D. Therefore, with no friction, the water would rise up and oscillate back and forth for ever. But, as argued above, friction will be extremely important so this oscillation will quickly damp out and will never rise up to a height equal to the depth of the ocean. See the video in the answer to the followup question below as an example for a miniature of this.

FOLLOWUP QUESTION:
Thank you for finding interest in my question and for being able to let the nuts and bolts slide. The calculations you created from my questions were like a body punch to my self esteem. I didn't understand a lick of it. And now I'm feeling like the Dickens character asking for more gruel. Your response knocked me for a loop. You pointed out two things I wasn't accounting for. The weight of the water in the tube and the air resistance. The air resistance I've resolved/incorporated. The equilibrium (if it occurs) from the weight of the water in the tube is a stopper and I hate it. Because it seems so common sense. Then I thought of this,(1000 ft.depth= 30 atmospheres = 420 psi.~), in your model if you bring the tube up at a 70 degree angle instead of the assumed 90, because of the longer tubing, there wouldn't be enough pressure to fill the tube. Also, if you put an uncapped tube from the surface to depth at a 70 degree angle as soon as you reached depth the tube would have too much water in it for the pressure and water would have to be expelled from the bottom until it reached the length of the 90 degree tube length. (I can't even do the baby geometry needed to figure out how much longer the tube would be.) Neither of these seems right to me. What do you think? What I picture happening is the moment the cap is removed at depth the whole ocean rushes to fill the void at the top and the water pressure at the outlet would be the same as at the intake. The entire tube would become an extension of the 420 psi zone at 1000 ft. If inside the tube was a vacuum and capped at the top wouldn't this be the case? Wouldn't the pressure be 420 psi at the cap? Here is my main reason for not being able to let this go. (this is my first version of this train of thought) Same long strong tube only this time it is assembled and capped in the vacuum of space 500 miles above earth and the capped end brought down to the surface. When the cap is removed I expect the atmosphere at that point to start rushing up the tube, through it, and out the end in a very long term geyser. And even though the tube is 500 miles long equilibrium would never be reached. Aren't both examples using the same principal? It seems to me that it is the same principal and that the water at depth would view this one atmosphere pressure at the surface as the next best thing to a vacuum and continue trying to fill it. Just as the tube from space would leak away our air. Doesn't pressure equal stored energy? This thought is like a song stuck in my head. I'm tired of thinking about it. It's been months now. Validation would be best for all but, at this point I would settle for a kill shot. Can you help (either way)?

ANSWER:
You have so many misconceptions that I am not even going to try to convince you with the physics arguments. A couple of comments: The reason that the pressure is so high deep in the ocean is that the water deep down must hold up the weight of all the water above it; to to try to ignore weight of the water in the tube misses the whole point. Suppose you had a tube 10 km long full of water (not underwater). The pressure at the bottom would equal to the weight of the tube of water divided by the area of the tube (+P _atm). Also, I have previously answered your question about the air in a tube in the atmosphere—it would not suck out all the air in the atmosphere for the identical reason your water tube would not create a perpetual geyser. Since you do not know any physics, let me convince you another way; remember physics, at its heart, is an experimental science, so let's do an experiment. Your idea should work equally well if the ocean were only 5000 m deep, maybe not just so robust a geyser, right? That is, your idea should scale. So, try the following experiment. Take a straw and put a little cork to plug the bottom and push it down into a glass of water; pop that cork out some way and see what happens. Does the water come up the straw and continually squirt out the top (tiny geyser) or does it come up to the level of the water surface and stop? Maybe it will rise a bit above the surface but it will settle back to the level of the water in the glass.

QUESTION:
Suppose we have a horseshoe magnet. Now we bend it in such a way that it becomes doughnut shaped and poles remain in contact with each other. In this situation what will happen to the magnet? Will it behave as a magnet? Where would be its poles? What will happen to domains inside the magnet?

ANSWER:
A horseshoe magnet is just a bent bar magnet, so let's start there. I have shown a short stubby bar magnet, but you can imagine that as it gets longer relative to its width the field inside will get more and more uniform. Now, bend it around into a circle and it will look just like a toroid. The magnetization inside will remain pretty much the same as before you bent it and there will just be field inside the torus, not outside. The domains will all stay pretty much the same.

QUESTION:
the Coriolis effect.. on a freely falling body... is to east...? motion of earth is towards east right.? so we must feel that falling body deflects to the west isn't it..???

ANSWER:
I cannot give the full derivation of the motion of a particle in a rotating coordinate system, it is much too involved. I can give you the results, though. The coordinate system we will use is the coordinate system (x',y',z') shown to the right. The Coriolis force is given by 2mv' x ω where v' is the velocity of m and ω is the angular velocity of the earth ( ω≈ 7.3x10^-5 s^-1). Now, for a body dropped from some height h, the direction of the velocity is in the negative z' direction, so the direction of v' x ω is east. This is not what you would intuitively suspect (as you note), but it is true. An expression for how far eastward it would drift before hitting the ground is x'=[( ω�cosλ)/3]√(8h ³/g) where λ is the latitude. For example, at the equator where λ=90⁰, and you drop it from 100 m, the deflection would be x'=2.2x10^-2 m=2.2 cm.

QUESTION:
What is impulse? My text book explains this as force acting for a short interval of time. Can you please explain this concept?

ANSWER:
What is the effect of applying a constant force F to a mass m? Newton's second law tells you that you cause the particle to accelerate, that is if you exert the force over some time t the velocity will change from v ₁ to v ₂. Writing Newton's second law, F=ma=m(v ₂-v ₁)/t. Rearranging this equation, Ft=m(v ₂-v ₁); so you can see that the amount which the product mv (which is called the linear momentum p) changes is numerically equal to the product Ft which is called the linear impulse J. If the force is constant, the time need not be short; t could be an hour and J would still tell you the change in p. I hope you can appriciate that J=p ₂-p ₁ is simply an alternative way to write Newton's second law. If F is not constant, you can still calculate J but it is just harder. In essense what you do is calculate Ft for many vanishingly small values of t all along the path the particle takes and sum them to get the total J. (If you know integral calculus, this is just integrating Fdt over the time interval.) Of course, Newton's second law is a vector equation, so J and p are vector quantities, J = p ₂- p ₁. If you have a system of particles which interact only with each other, the net force on the whole system is zero because of Newton's third law, so J =0 and p does not change as the system moves around; this is called momentum conservation. Here p means the momentum of the whole system, the vector sum of all the momenta of all the particles.

QUESTION:
I've started reading an elementary particle textbook and it doesn't explain why a moving charged particle radiates an EM field. I was hoping you could help with that.

ANSWER:
The semantics of "radiates an EM field" is somewhat ambiguous. A charged particle at rest creates a static electric field. A charged particle moving with constant velocity (constant speed in a straight line) creates both an electric field and a magnetic field and both change with time. But neither of these situations are said to radiate electromagnetic fields. Electromagnetic radiation propogates through space as waves; visible light, for instance, is an electromagnetic wave. Electromagnetic fields can be created when a charged particle accelerates. E.g., an antenna radiates radio waves when electrons in the antenna are made to oscillate back and forth (accelerating). The derivation of how accelerating charges radiate is a topic in an intermediate E&M course and beyond the scope of this site.

QUESTION:
In the famous book by H.G Wells - "The Invisible Man" - the invisible man explains that his invisibility is due to light getting passed through a membrane (his skin/tissue) clearly , i.e not reflecting or refracting. Is this true? Can a object me made invisible by this method? Further, has there been some actual research in this topic and any advancements?

ANSWER:
First, it is not "true" —this is a book of fiction! More pertinently, is it possible? I would say, given what we know today, it is not possible because for the light to not be refracted the speed of light in the body would have to be the speed of light in a vacuum, and there is no material for which this is true. Research regarding invisibility is focused on "invisibility cloaks".

QUESTION:
A charged parcticle when accelerated radiates electromagnetic radiation or light. All atoms on earth are accelerated therefore the electrons and protons which are charged are also accelerated so why isnt light radiated?

ANSWER:
First of all, atoms are neutral, have zero net charge. Second, the accelerations involved because of the earth's motion are very small.

QUESTION:
Why does centripetal force do what it does? It is a force so why does the object start moving in a circular path and not simply in the direction of the force? Also it should provide acceleration...so even if some how the object move in circle why doesnt it spiral in??

ANSWER:
If an object is at rest and you exert a force on it, that force will not cause the object to "start moving in a circular path". You cannot simply label something a centripetal force. If an object is moving in a circle with constant speed, it is accelerating because the velocity is constantly changing. The velocity vector can change either by changing its magnitude (speed) or its direction. An object moving in a circle therefore requires some force to accelerate it, for example the sun's gravitational force on the earth, which points toward the center of the circle. If you stopped the earth in its orbit, the gravitational force would indeed cause the earth to crash into the sun. You need to simply look up a derivation of centripetal acceleration in any elementary physics text you would understand this better.

FOLLOWUP QUESTION:
unhuh...
how can it change direction without changing its magnitude??

therefore in time dt the velocity in downward direction becomes adt

where v' is equal to the vector sum ie v'=((v)^2+(adt)^2)^1/2, so how is the velocity supposed to be constant when the object is not decelerating tangentially?

ANSWER:
Like I said in my original answer, look this up in an elementary physics text — I am not a tutor. The reason your argument is invalid is that dt is infinitesimal so if a dt is perpendicular to the velocity vector v , the result is to change direction. (Limit(as dt —> 0){ √[v ² +(adt)²]}=v.) Just use your common sense: a car going in a circular path has a constant magnitude of velocity, right? And nonconstant direction or velocity, right?

QUESTION:
Two bodies A and B are at rest and in contact with each other. Now if some arrangements made body A exerts a pressure of 10 NEWTON on body B then according to NEWTON'S 3rd law of motion body B will also exert an equal force of 10 NEWTON in opposite direction so the resultant force should be zero, while practically we see that there will be a resultant force of 10 NEWTON acting on body b and if mass and other conditions of body B are such that it moves by applying 10 NEWTON force on it. Then it will start moving. HOW?

ANSWER:
You have this all confused. But, you are not alone! When doing this kind of problem, you must choose a body to focus on; only forces on that body affect its motion. So, if you are interested in what body B will do, you look only at that body. The force which B exerts on A is not a force on B. So, if B has a mass of, say, 2 kg and there are no other forces on B, it will have an acceleration of a _B=10/2=5 m/s². Since the 10 N force continues, A and B remain in contact, so a _A must also be 5 m/s². One force on A is the 10 N force from B which is in the opposite direction as the acceleration. But the net force on A must surely be in the direction of the acceleration, so there must be some other force (probably due to you pushing on A) on A which is bigger than 10 N and points in the direction of the acceleration. For example, if the mass of A is 4 kg, F-10=4x5=20 N, so F=30 N. Finally, you could look at A and B together as the body. In that case the forces they exert on each other do cancel, the acceleration is 5 m/s², and the total mass is 6 N; therefore, there must be some external force (you again) causing this 6 kg to have an acceleration of 5 m/s²: F=ma=6x5=30 N. All three ways of looking at this problem are consistent with each other.

QUESTION:
Can I make a simple bike reflector using 20 thru 40 degree angles? Everything I have read uses 45 and 90 degree angles.

ANSWER:
I do not know how 45⁰ would work. The point is for the incident light to be reflected in exactly the opposite direction from the direction it came in. The only way I know to achieve this is with corner reflector which is three mirrors connected as in the inside corner of a cube.

QUESTION:
Why simple harmonic motion is called simple?

ANSWER:
Take a look at the figure above. The red curves are all pure sine waves, just having different frequencies. These are all called simple harmonic motion because they may be expressed as a single sine wave. Now, take all four of these and add them together. The result is the black curve. This curve is still harmonic (which means that it is periodic, it repeats itself after some time, called the period, has elapsed) but it is not "simple" because to describe it you must use four different sine waves.

QUESTION:
I am a Martial Arts instructor who also happens to have a BS in mathematics (well, statistics, sorta like math). I like to explain to my students the science of the art in order to help ground them in reality from a lot of the BS involved in Eastern Mysticism, such as board breaking. My question is this, wooden weapons, such as nunchaku are usually either round/cylindrical or octagonal. A common technique is to place the weapon lengthwise down the arm and block an incoming attack with the wood. Traditional tonfa are octagonal, but modern police batons (with the side handle) are round. Which would protect the blocking arm from a baseball bat strike (for example) to a greater degree? Would an octagonal shape disperse the incoming force more than a round shape? I believe the octagon would spread the applied energy to a greater degree than a cylindrical/round shape and allow less energy to travel through the wood and into the arm, but I cannot find the math to back this up.

ANSWER:
The only reason that I would say that the octagonal shape would be better is that it has a larger area of contact with the arm and therefore would distribute the applied force over a larger area. For example, you would not just want a point in contact with the arm since all the force would be applied at a single place. Even better in this regard would be a rectangular shape. This is probably a negligibly small effect, though. I cannot see how the shape would have any effect as you suggest to " … allow less energy to travel through the wood …"

QUESTION:
How much energy is required to move the electron sufficiently far away from the proton such that it does not experience the proton's electric field. I am kind of confused by this question. The effect of electric field will never end as far as we take the electron from the proton. And if we use the relation V=E.L then if E=0, then L will be infinity?

ANSWER:
Technically, yes the field will be exactly zero only at L= ∞. But, that is only if your proton and your electron are the only things in the universe! You can calculate the ionization energy, the energy necessary to move an electron from the ground state of hydrogen to infinity; it is 13.6 eV=2.18x10^-18 J. You can also calculate the energy necessary to move it to any other distance. For example, the energy to move it to about 0.5 μ=5x10^-7 m (which is about 100 times the radius of the hydrogen atom) is 13.599 eV, essentially the same as to infinity. So you can see that most of the energy is supplied in close to the proton because that is where the field (and therefore the force) is strongest.

QUESTION:
So I've been trying to figure this for a while, if a positively charged and a negatively charged quark orbit each other or actually come in contact, also could they form a functional "atom" and be able to have electrons interact with them?

ANSWER:
Two-quark particles are called mesons (one quark plus one antiquark). If you had a positively- and negatively-charged quark you would have an uncharged meson and so it would not bind an electron and you could not have a meson+electron atom. However, if you had a positively charged pion, it could bind an electron. For example, a positive pion π ⁺ is composed of an up quark (charge +2e/3) and a down antiquark (charge +e/3) and would have a charge +e and be able to form an "atom" which you might call pionium.

ADDED NOTE:
Whoops! Pionium is an "atom" composed of one π ⁺ and one π ^-. I cannot find any reference to this pion+electron system, so I guess you can call it whatever you like.

QUESTION:
i love physics and this question i asked to my teacher and principal but they couldn't answer it so my question is about third law of motion "every reaction has an equal and opposite reaction" so when a truck moving with constant speed hits a stationary car so according to newton's 3rd law of motion truck shoud be stopped after collision because car applies equal force on truck which it have during collision.

ANSWER:
Why should it be stopped? Certainly the truck experiences the force which the car exerts on it, but every force does not have the effect of stopping the object which experiences a force. If you are running toward a fly which is hovering at rest in your path, you feel the force of the fly but it does not stop you.

QUESTION:
Hi ...here is a link to Felix Baumgartner's freefall jump from space - https://www.youtube.com/watch?v=vvbN-cWe0A0 135,890 feet - or, 41.42 km (25.74 mi) In the video you see speed at which he is supposedly travelling, 729 mph (1173km/hr), 46 seconds after he jumped. The footage is cut then seconds later speed strangely falls to 629 mph...anyway after 4 mins and 18 seconds of free falling he releases parachute. My questions are What speed would he be going at a 4 mins and 18 seconds into freefall? Also how do you explain the deacceleration when it was at 729 mph then down to 629 mph?

ANSWER:
(You might be interested in an earlier answer.) There is a better video at https://www.youtube.com/watch?v=raiFrxbHxV0; this video shows data acquired by instruments on Baumgartner. Here some clips from that video:

The first three are the times also showing speeds; these are roughly the speeds you refer to in your question. The second three show speeds and altitudes. The third graph shows the whole history of altitude, speed, and mach speed. The speeds are all larger than indicated in your video. The speed at 4:20, 113 mph, answers your first question. The speed at 0:50 is about the maximum, 847 mph or mach1.25. The speed at 1:01 has dropped to 732 (about the same change as your video); I suspect this deceleration is due to two factors: there is getting to be much more air resulting in higher drag and, probably after he broke the record he oriented his body to increase drag and slow down. The official maximum speed after everything was calibrated was 843.6 mph.

QUESTION:
Will the drag coefficient be the same in air and water?

ANSWER:
There is no simple answer to this question. The drag coefficient C _Dis a constant characterized by the geometry of an object used to calculate the drag force F _D if it is proportional to the square of the velocity v: F _D= Ѕ C _D ρAv ² where A is the area the object presents to the fluid flow and ρ is the density of the fluid. Whether or not this equation is true depends on a quantity called the Reynolds number Re=L ρv / η where L is a length along the direction of flow and η is the viscosity of the fluid. It turns out that only if Re>1000 is the velocity dependence approximately quadratic. If Re<1 the drag force is approximately proportional to v. Anywhere between these extremes the drag force is a combination, F _D ≈Ѕ C _D ρAv ²+kv. C _D ≈constant only for the case Re>1000; the drag coefficient would then be the same for identically shaped objects. It is interesting, though, to get a feeling for what the relative speeds in air and water corresponding to Re=1000 are. The necessary data at room temperature are ρ _air≈1 kg/m³, ρ _water ≈1000 kg/m³, η _air≈1.8x10^-5 Pa�s, and η _water≈1.0x10^-3 Pa�s. Then v _water/v _air≈(1.0x10^-3/1000)/(1.8x10^-5/1)=0.056 (which is true for any Re). Taking a sphere of diameter 0.1 m as a specific example for the critical Re=1000, C _D=0.47, A=7.9x10^-3 m², L=0.1 m, v _air=1000x1.8x10^-5/(0.1x1)=0.18 m/s and v _water=1000x1.0x10^-3/(0.1x1000)=0.01 m/s. Since the speeds are relatively low, you can conclude that for many cases of interest the quadratic drag equation holds for both water and air. Therefore, for many situations you can approximate that the drag coefficient in air and water are about the same. For a specific case you should check the Reynolds numbers to be sure that they are >1000. The bottom line is that if the drag force depends quadratically on velocity, the drag coefficient approximately depends only on geometry, not the properties of the fluid. Keep in mind that all calculations of fluid drag are only approximations.

ADDED COMMENT:
As I said above, for 1<Re<1000, F _D ≈av+bv ²where a and b depend on Re; e.g., a≈0 for Re>1000 and b≈0 for Re<1. So, for Re<1, a is just a constant and F _D≈av≡Ѕ C _D ρAv ² so C _D=2a/( ρAv )=2aL/(A ηRe )≡c/Re where c is a constant. If F _D is proportional to v, C _Dis inversely proportional to Re; this is called Stokes' law. As we saw above, Re>1000 leads to C _D=constant. Ferguson and Church have derived an analytical expression which very neatly reproduces data for the transition from Stokes' law (1/Re) to constant C _D. Calculations for a golf ball are shown at the left (constant C _D, the green line, is called turbulent in the legend). Note, as we have stated, that the transition occurs in the region 1<Re<1000. Note the sudden drop in the data around Re=500,000. I believe that this must be due to the dimples on the golf ball which reduce drag.

QUESTION:
In induced magnets, why does the end nearer the magnet have the opposite polarity to that of the magnet?

ANSWER:
Think about a piece of iron. It is like a whole bunch of tiny bar magnets, each of which has a N and S pole; but the iron is usually not a magnet macroscopically because all the tiny magnets are oriented in random directions. But, if you bring the north pole of a permanent magnet up close to the iron, the south poles of all the tiny magnets turn to point toward the north pole of the permanent magnet.

QUESTION:
I think if an object is turning, it has more gravity than an object which is not turning

ANSWER:
You are right. However, it really has nothing to do with the turning, per se. When something is turning it has rotational kinetic energy and therefore a spinning planet has more energy than an otherwise identical planet not spinning. In general relativity you usually hear about gravity being caused by mass warping spacetime. However, mass is just the most obvious source of gravity and what it is which really warps spacetime is energy density and mass has a lot of energy (E=mc ²). The energy due to the turning is infinitesmal compared to the mass energy of the object so you would never be able to distinguish the difference due to the turning by looking at the gravity.

QUESTION:
I've heard that a bullet falls to the ground ~~at the same speed~~ [in the same time] no matter the charge pushing it forward. More powder and it moves faster but vertical speed is the same. I imagine two equal weight gliders of 20/1 and 30/1 lift/drag ratios would also express the same vertical speed? My question is, wouldn't this gravity effect also hold true underwater? An underwater glider expressing 30/1 L/D would travel 50% further, faster than a 20/1 L/D in a given vertical?

ANSWER:
I will assume that we are talking about horizontally fired bullets. All bullets do not hit the ground with the same speed, rather they all take (approximately) the same time to get to the ground; I have corrected your question because I believe that is what you meant. Your comparison to gliders with different lift/drag ratios is not appropriate, because the thing which results in the times of vertical fall being the same is the assumption that there is no lift at all. In other words, the vertical speed of a bullet will always be much less than the terminal velocity so there is no appreciable component of the drag in the vertical direction. (This is not true if the gun is fired from a very high altitude since there will be enough time for the verticle component of the velocity to approach the terminal velocity.) Underwater (I am just talking about bullets, not gliders) the bullet will not behave the same because the terminal velocity is much smaller than in air, in other words the drag is much larger.

QUESTION:
Quantum mechanics has popularized the idea of very small particles existing in two or more points in space during the same instant in time. Is this to be taken at face value as a fundamental aspect of quantum particles, or is this simultaneous existence just a concept used to express our inability to observe these particles without inadvertently altering their speed or location?

ANSWER:
See an earlier answer.

QUESTION:
I read from my history book that when nukes were first created we didn't know that the radiation their explosions produce is harmful to one's health, even to one's life maybe. So my question is, how come neither physicists or medical personnel ever figured out that radiation can be dangerous until we had first victims of radiation?

ANSWER:
Ever hear the expression "hindsight is 20-20"? It is unrealistic to expect that when something new is discovered that we should somehow know all the effects that might have on anything else. At the time radioactivity was discovered, nobody even knew what atoms were composed of or what their structure was. And it was found to be very tiny bits of matter (e.g. what we know as electrons today) and who would have thought that getting hit by something trillions of times lighter than a speck of dust could be harmful? It took experience before it was appreciated how dangerous it could be. One of the best known examples of such experience is the case of radium watch dials. Radium, mixed with a phosphor, was painted by women onto watch dials and it would glow in the dark. The workers were encouraged to point their brushes with their lips to make the fine lines required. Subsequently many became ill with cancer and other radiation sickness. It seems stupid now, but the dangers were not known until they were discovered. Also many of the health effects were long-term effects, the effects not appearing until years or decades after exposure. One example I know about from personal experience is the effect of radiation treatment for acne which was popular in the 1950s. I very much wanted to have this done but my father forbade it, making me furious with him. Years later people who had had this treatment started coming down with cancer —thanks, Dad! Yet another example is the shoe-fitting x-ray machine. When I was a kid it was really fun to buy new shoes because you could look down at an x-ray of all the bones in your foot and how well the shoe fitted you; again, when more was learned about radiation, these machines were all sent to the scrap heap. When it began to be appreciated that there were dangers, studies began to be done to try to set allowable dosage levels. But, it is unethical to do such experiments on people, so lab animals had to be used which always presents problems with scaling and other variables. Much of what we know today was learned after-the-fact by doing long-term statistical analyses over decades of medical records.

QUESTION:
Magnetic flux according to my book is total no. of magnetic field lines passing through a given area in magnetic field. ok but why there are not infinite no. of magnetic field lines, because magnetic field line are defined as the path that a magnetic north monopole would take if left in north part of magnet, so if i take a monopole and leave one atom away from the previous position then it should take a slightly different path and that path should be considered as magnetic field line,so in this way i can draw millions of line.

ANSWER:
Magnetic flux is well defined: Φ _M≡∫∫ B �d A , the area integral of the magnetic field. If the integral is over a closed surface, the flux is zero; this is the famous situation which tells you that there are no point sources (called magnetic monopoles) of magnetic fields like there are for electric fields. If you like, you may interpret this as a number, but that is not really fundamental. If you talk about uniform magnetic fields which are perpendicular to a plane surface, Φ _M=BA , is the flux through an area A. Then, if you interpret Φ _M as a number, you would simply say, for example, there were 10 lines through an area of 1 m² if the magnetic field is 10 T. You could ask the same question about electric flux, Φ _E≡∫∫ E �d A . This is perhaps a little easier to understand because you can have point charges. For example, if you have a 1 C point charge, the electric field 1 m from it is E=Q/(4 πε ₀ r ²)=1/(4x3.14x8.85x10^-12x1²)=9.27x10⁹ N/C. The flux at a distance of 1 m from the charge would therefore be Φ _E =EA= 9.27x10⁹x4x3.14x 1²=1.17x10¹¹ Nm²/C. Incidentally, this is the flux regardless of where you measure it because the area of the sphere (4 πr ²) surrounding the point charge appears both in the denominator of the field and in the numerator of the flux and cancels. Hence, you could say that there were 1.17x10¹¹ lines of electric field emanating from a 1 C point charge. You can see this from Gauss's law, Φ _E=∫∫ E �d A =Q/ε ₀ if the integration is over a closed surface enclosing the charge Q.

QUESTION:
Why degree of monochromaticity is always non zero?

ANSWER:
The practical reason is that you cannot make a laser which is perfectly free from electronic instabilities and noise. But even if you were able to make a perfect laser, you could not know its frequency perfectly. The more fundamental reason is that monochromatic light means light with a single frequency. But, the linear momentum of the photons is proportional to the frequency of the light. Because of the Heisenberg uncertainty principle, the only way you can know momentum of the particle perfectly is to be completely ignorant of its position; you need an infinitely long wave to know its frequency perfectly.

QUESTION:
This question is about relativity. If person leaves earth and heads toward a star that is 10 light years away, and he travels at near the speed of light, time will slow down for him. The round trip to the star may take him only one year, but when he returns, maybe 100 years have passed on earth. When he started out to the star, he knew it was 50 [I think you meant 10, right? The Physicist] light years away. It seems that for him, he will have traveled 20 light years in one year. That is faster than the speed of light. What don't I understand?

ANSWER:
First of all, time for the traveler will not slow down; rather, her clock will run slower as observed by an observer on the earth. To her, time will run perfectly normally. However, she will observe the distance to the destination shortened because of length contraction. You have rounded things to what they would be if she were going the speed of light, but let's do the whole problem as if she were going with a speed v=0.999c. The earth observer would see an elapsed time of 100x0.999=99.9 years (your 100 years). The traveler will see the distance shrunk to D'= 10 √(1-.999²)=0.447 light years, so the time of travel is t=2x0.447/0.999=0.895 years (your 1 year). You should read the earlier answer on the twin paradox.

QUESTION:
Supposing a weightless container is filled with water. I am sure the pressure at the bottom of liquid, P1 = atmospheric pressure + height of liquid x density of liquid x g = Patm + hdg, where Patm is atmospheric pressure and d is density of liquid. We can calculated this pressure as if liquid in region A and Region C does not exist. But how about the the pressure at the base of the container, that is P2. Is P2 same as P1? For P2, do we need to consider the whole weight of the liquid, that is inclusive of the weight of water in region A and C?

ANSWER:
It depends on what the force on the bottom is. If the container is in equilibrium, imagine it sitting on a table. The table would exert an upward force equal to the weight W of all the water, so P ₂ would be W/A _bottom where A _bottom is the area of the bottom of the container. This assumes that atmospheric pressure is the same everywhere in the vicinity of the container; in other words, I have ignored the buoyant force due to the air on the whole container because it will surely be much smaller than W.

FOLLOWUP QUESTION:
Indeed the container is resting on the table. For P1, I use h x d x g. But for P2 you use W / Abottom, So can I say P1 not equal to P2 ?

ANSWER:
Yes, but I have to admit that my answer was misleading in that I gave you the gauge pressure, the pressure above atmospheric. So I should have said that P ₂=P _atm+W/A _bottom. There is no problem that P ₂ ≠ P ₁ because the force which the container exerts on the table is not P ₁ A _bottom. Think about it —the sides of your container exert a downward force on the bottom of the container.

QUESTION:
Think of words (incapital letters) that can be read properly both with a mirror and without a mirror. What are these words?

ANSWER:
Well, this is not physics and I usually do not answer such questions. However, it is a cute puzzle. First, any letter in the word which is symmetric upon reflection about a vertical axis will look the same in the mirror: A, H, I, M, O, T, U, V, W, X, Y. Second, any such word must be a palindrome composed of the allowed letters, e.g. AHA, OTTO, WOW, YAY, MOM, TIT, TUT, … . But, wait, it is somewhat more difficult than that! Look at the pictures of the Camel cigarette package and its reflection, in particular, the word CHOICE on the side. So words composed of letters with symmetry upon reflection about a horizontal axis will also reflect the same: B, C, D, E, H, I, K, O, X will have a reflection which is the same as the original, but only if turned upside down. There is no restriction for these words to be palindromes; besides CHOICE, some others would be BED, HEX, BOX, BIKE, HIKE, CHIDE, …

QUESTION:
What is meant by virtual image?

ANSWER:
It is an image formed by light which appears to be coming from somewhere but is not actually coming from there. When you look into a mirror, it appears that the light from the image of what you are looking at is coming from behind the mirror, but it is actually coming from the mirror itself.

QUESTION:
Supposing that initial velocity is 0 Is a displacement vs. time (squared) equivalent to a Velocity vs. time graph? I tried to find the slope of displacement-time^2: d/t^2 = V/t which equals acceleration But what I read everywhere is that: d/t^2 = a/2 according to the equation d= (initial V)(time)+ (1/2)(at^2) I don't what is wrong with my calculations?

ANSWER:
If you plot d vs. t ², the slope of the line will be Ѕa. You know that d=Ѕat ², so suppose that I call t ²=u. Then clearly the slope of the line d=Ѕau is Ѕa. Your equation d/t ²=V/t is clearly wrong: d/t ²= Ѕat ² /t ²= Ѕa and Ѕa≠v/t.

QUESTION:
Two of us disagree on part of a sol'n given by two people with Physics background, and I want to know if I am correct, or if I am missing something in the analysis of the problem...in case I have to explain it to a student. Question concerning Forces/impulse..... 50kg person falling @15m/s is caught by superhero , and final velocity up is 10m/s. Find change in velocity. Find change in momentum . It takes 0.1 sec to catch them.....ave Force is ? answers are: vel = 25 m/s change in mom.. 1250 kg*m/s, and ave Force = 12,500 N. Here's where we disagree: Person B says that 12,500 N is equiv. to 25 g ????? They try to explain that 250 m/s^2 accel. corresponds to 25g.... I said it makes No sense at all, [ I know the accel. is 250, but that doesn't in any way imply a 25 g "equivalence" to me ]. They then went further to "prove" their point........Here is their argument... 500 N/g = 12500N / ( )g ..... I agree the ( ) = 25, but say there is No justification for the 500 N / g in the first place...... any ideas where it comes from , or how to justify that value ? BTW I teach physics on and off at the HS level.... person B is an Engineer , I think

ANSWER:
Person B is wrong but has the right idea. (As you and your friend have apparently done, I will approximate g ≈10 m/s².) We can agree that the acceleration is a=250 m/s² and that is undoubtedly 25g. Now, we need to write Newton's second law for the person, -mg+F=ma=-500+F=12,500, so F=13,000 N. This is the average force by the superhero on the person as she is stopped, so the answer that the average force is 12,500 N is wrong. When one expresses a force as "gs of force", this is a comparison of the force F to the weight of the object mg, F(in gs)=F(in N)/mg=13,000/500=26 gs; this simply means that the force on the object is 26 times the object's weight. So neither of you is completely right, but if there is any money riding on this, your friend should be the winner because the only error he made was to forget about the contribution of the weight to the calculation of the force. I am hoping that superman knows enough physics to make the time be at least 0.3 s so that Lois does not get badly hurt!

QUESTION:
It is said gravitons are the expected particles to exchange the gravitational force. Do these particles exist in real?

ANSWER:
There is no successful theory of quantum gravity, so gravitons are "expected particles" but I would not call them "real" at this stage; hypothetical would be a better word.

QUESTION:
Why does it take more time to go to Dubai from Mumbai than to come from Dubai to Mumbai?

ANSWER:
There are winds at high altitudes called jet streams. The prevailing direction of these winds is easterly and their speeds are as large as 100 mph. Therefore when you travel east (as from Dubai to Mumbai) you have a tail wind, and when you travel west (as from Mumbai to Dubai) you have a head wind. Since the greatest speed an airplane can fly, say 600 mph for commercial jets, is airspeed, that is relative to the air, the ground speed with a 100 mph wind would be 700 mph going east and 500 mph going west.

QUESTION:
Why is the direction of angular displacement along the rotational axes?

ANSWER:
There are two ways in which you can rotate something about some axis, either clockwise or counterclockwise (as viewed from one side or the other). So, an angular displacement has two possible directions only. It is like a displacement in one dimension, like a bead on a long straight wire. You then call one direction on the wire plus and the opposite direction minus. The only way to get a similar directional assignment for a rotation is to note that the rotation axis is just like a one-dimensional axis, one way being assigned to be positive, the other negative. Usually this is done with the right-hand rule such that counterclockwise is a positive vector on the axis.

QUESTION:
Recently I came across such an article that Gravity isn't actually a Force, It's the bending of space-time that cause objects to move on curve paths. If two objects of equal shape and masses are there they will bend the space-time in same way by same amount. Then according to that there shouldn't be any kind of force or something acting between them which isn't true i guess. Gravity forces will act b/w those two. Could you please explain me this contradiction.

ANSWER:
I do not understand your logic that because they both have the same effect on spacetime, they will feel no force. Although it is just a cartoon to help you qualitatively understand warping of spacetime, in this case it is illustrative. If you place a bowling ball on a tranpoline, what happens? The surface of the trampoline is warped. Now, suppose that you place two bowling balls a few inches apart from each other. What happens when you let go of them? They will behave as if there were a force between them and roll toward each other but what they are really doing is responding to the shape of the trampoline.

QUESTION:
I have a question about gravity, or more specifically how to calculate it for the purpose of a scifi fanfiction I am making. So Earth has the density of 5.5 grams per cubic centimeter, total mass of 5.97219Ч10²⁴ kilograms and radius of 6371 kilometers. So how do I put these together in a formula to get the 9.81m/s gravity?

ANSWER:
The density is irrelevant. You need to use Newton's universal law of gravitation for two point masses. The force F which each feels is F=GMm/r ² where G is the universal gravitational constant, G=6.67x10^-11 N � m²/kg², M and m are the masses of the two masses (take M as the mass of the earth), and r is the separation between M and m. This also works if the masses are spherically symmetric. But, of course, you also know in your case that F=mg. So, if you solve for g, g=MG/r ² ≈ 6.7x10^-11x6.0x10²⁴/(6.4x10⁶ )²=9.8 m/s².

QUESTION:
Why do electrons fall back to the ground state after jumping into a higher orbital?

ANSWER:
The simple answer is that a system will always seek a way to move to a lower energy, like a ball rolling down a hill and not up it or sitting still. The more complicated answer addresses whether there is, indeed, "a way" to achieve this. For atoms, the radiation of photons in the transition is usually electric dipole radiation and there is a corresponding quantum-mechanical operator, let's call it O _E1. Then, you have to look at what is called the transition matrix element for this operator, < Ψ| O _E1 |Ψ'>=∫Ψ� O _E1 �Ψ'dτ which is an integral over all space and Ψ' and Ψ are the excited and ground states, respectively. If this is nonzero, then the decay will decay with some half life determined by the value of the matrix element. If it is zero, the state will still probably decay to the ground state but via a different kind of transition.

QUESTION:
We all know about second law of motion. The example is about the coin which is placed above the cardboard and cardboard is placed above the beaker... if the cardboard is quickly pulled then the coin falls in the beaker but if the cardboard is slowly pulled then why does the coin come with the cardboard? Why does this happen?

ANSWER:
This is usually used to demonstrate inertia, Newton's first law; since you are interested in why it does not work if you move the cardboard slowly, the second law also must be used. To move the cardboard from rest it must experience some acceleration. If the coin is to experience an acceleration, that is move with the cardboard, some force must be exerted on it. The only force on the coin horizontally is the static friction and the greatest it can be is μmg (where μ is the coefficient of static friction) so the greatest acceleration the coin could have is μg; for example, if μ=0.3, and you caused the acceleration of the cardboard to be any greater than about 3 m/s², the cardboard would slip under the coin. But, if you gave the cardboard an acceleration of 0.2 m/s² the coin would move with it.

QUESTION:
How can it be said that the universe is only 13.7 billion years old? This seems ridiculous to me that anyone can make this assumption. Taking in the fact that there are black holes almost as old as the universe itself how is this possible? Stars live billions of years so the first group of black holes would be billions of years after the "big bang". Also due to the fact that the universe is expanding way faster and not slowing down like predicted it would seem to me the current model is wildly inaccurate. Can you please explain this to me? My understanding is that stars form and die out all the time so to be able to accurately determine the age of the universe another method would need to be devised. It is my understanding that galaxies form with the help of super massive black holes.(Which aren't even holes at all but super compacted spheres of matter so dense light cannot escape created by countless other bodies of mass.) Which attracts matter into tight clusters of stars we call galaxies. These galaxies would have to take billions of years to form after the creation of the first stars ever created and after the first black holes were created from some of those stars. Does the current model explain this?

ANSWER:
As clearly stated on the site, I do not do astronomy/astrophysics/
cosmology. I can at least say a little about your question, though. The age of the universe is not an "assumption", it is based on careful analyses of many measurements. The stars in the early universe were much more massive than the sun; this resulted from the fact that the early universe was essentially all hydrogen and a bit of helium. Stars began forming only 100-200 million years after the big bang. Very large stars burn much hotter than smaller stars and therefore have much shorter lifetimes, a few million years rather than a few billion years for less massive stars (e.g. the sun with an expected lifetime of about 10 billion years) which would explain why many black holes are very old. The rate of expansion of the universe is not inconsistent with the model of a big bang about 14 billion years ago (in fact, the rate is one of the measurements used to estimate the age of the universe) even though we do not understand all the details (e.g. dark energy and accelerating expansion).

QUESTION:
I would like to ask this question because I do not agree to this but it is written in my school handout. It says that work needs only two things to be calculated which is weight and height of displacement. Now , there is this question that says that two persons who have the same mass went to the top floor of eiffel tower. One used the stairs and the other one used an elevator. The thing is that our handouts states that they both exerted the same amount of work done because they have the same weight and they both have the same height distance covered. I do not agree simply because the man using the stairs carried his own weight up the distance while the the other one was being carried by an elevator and I immediately thought that the elevator was the one doing the work and not the person which is why they cannot have the same work done. If I am wrong then I would humbly accept it. However , if our physics teacher is wrong, I would need a legit source stating about the problem and saying that it was wrong or similar problem like the one given with an answer so I can correct my grade. I would really appreciate anyone's help right now.

ANSWER:
The point is that the net work done on each person was the same. Where the energy came from is different. On the stairs, the energy is supplied by what the guy ate for lunch. In the elevator, the energy is supplied by the motor lifting the elevator. Regardless where it came from, mgh of energy must be somehow supplied.

QUESTION:
How surface tension overcome insect weight and help it to stay on liquid surface, as surface tension is along liquid surface?

ANSWER:
The weight of the insect causes the water to be depressed where the legs touch the surface, so the surface tension has a vertical component.

QUESTION:
Can we make something like anti-gravity on Earth, or something similar to that? And i was wondering if we could make something like anti-gravity with magnets, to actually reduce the weight of some object. I was thinking to make a chamber with a magnet at the bottom, and take magnetized objects and put them on the top, so it will levitate.

ANSWER:
Your device will not work. The magnet on the bottom can be made to exert a repulsive force on a magnet at the top which tends to lift your chamber. However, Newton's third law requires that the top magnet exerts an equal and opposite force on the bottom magnet, so the net force on the chamber is zero.

QUESTION:
Is rotation a reason for earth being round?

ANSWER:
No. The reason that all large astronomical objects are nearly spherical is because the force which holds them together is spherically symmetric. If you have a point mass, the gravitational force another mass feels depends only on how far apart they are, not on the direction. If you want a lot more detail, see an earlier answer about gravity of a cylinder which shows how the tendency is toward a spherical shape.

QUESTION:
Using a spring balance, weigh (separately) a piece of wood and a container with water in it. Then weigh them again, but with the wood floating in the water. Does the reading on the balance change? There will be an upthrust on the wood (Archimedes' Principle), causing it to weigh less. I guess there will be an equal down-force exerted by the wood, resulting in the same weight being shown in both cases. This seems a fairly easy question, but I can't find the answer clearly stated anywhere.

ANSWER:
The measured weight will be the sum of the individual weights. The buoyant force is the force which the water exerts on the wood; Newton's third law requires that the wood exert an equal and opposite force on the water. As you correctly "guess", these two forces cancel out.

QUESTION:
Good afternoon. I started learning quantum mechanics and I have a question about Heinsenberg's principle. I was thinking about a photon created by an electron-pozitron annihilation. As I understand (and I hope I am not wrong here) all observers, no matter their state, can specify the point (and all will specify the same point) where the photon appears, and I think in a Wilson chamber we can do this thing. Anyway, we can specify its position with an error less than infinity. But at the same time we know it's speed with absolute precision, as, assuming we measure it in vacuum, it's speed is invariably c. So the product between (delta)x and (delta)p will be 0, as (delta)x is not infinity and (delta)p is 0. In other words we can predict it's position with a certain accuracy knowing at the same time it's speed (I am not sure, but i think that the (delta)p is not a vector but a scalar quantity). What is wrong about this as it seems the Heinsenbrg's principle is violated?

ANSWER:
The mass of a photon is zero but it has momentum. Therefore your notion that linear momentum p is mass m times velocity v must be wrong; the relativistically correct expression for momentum is p=mv/ √[1-(v/c)²] where c is the speed of light. For a photon, this is a little tricky because p=0/0, but you can also write that E ²=p ² c ²+(mc ²)² where E is the energy of the a particle of mass m, so p=E/c if m=0; since E=hf for a photon, where h is Planck's constant and f is the frequency, the linear momentum of a photon is p=hf/c . Therefore the frequency of the photon must be uncertain according to the uncertainty principle. Since the energy of a photon is hf, there will be an uncertainty in the energy of the photon.

QUESTION:
The units of the Hall coefficient is m^3/C that's, cubic meter per coulomb. How so we get this?

ANSWER:
You just need to know the definition of the Hall coefficient R _H, R _H ≡ V _H t/(IB) where V _H is the Hall voltage, t is the thickness of the sample, I is the current, and B is the magnetic field. The Hall voltage may be shown to be V _H=-IB/(nte) where n is the charge carrier density (units [m^-3]) and e is the charge (units [C]]) of a charge carrier. Therefore R _H=-1/(ne) so the units of R _H are m³/C.

Find All Solutions to the Equation 2sinî¸20

Source: https://m2.askthephysicist.com/ask_phys_q&a_old8.html

Wickham Whines

Find All Solutions to the Equation 2sinî¸20

Menu Halaman Statis